Problem B. 5058. (November 2019)

B. 5058. Let \(\displaystyle P\) be an arbitrary point in the interior of triangle \(\displaystyle ABC\). Lines \(\displaystyle AP\), \(\displaystyle BP\) and \(\displaystyle CP\) intersect sides \(\displaystyle BC\), \(\displaystyle AC\), and \(\displaystyle AB\) at points \(\displaystyle A_1\), \(\displaystyle B_1\) and \(\displaystyle C_1\), respectively. Prove that

\(\displaystyle \frac{AP}{A_1P}\cdot\frac{BP}{B_1P}\cdot\frac{CP}{C_1P}\ge 8. \)

Proposed by L. Németh, Fonyód

(4 pont)

Deadline expired on December 10, 2019.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A \(\displaystyle PBC\), \(\displaystyle PCA\), \(\displaystyle PBA\) háromszögek területe legyen rendre \(\displaystyle a\), \(\displaystyle b\), illetve \(\displaystyle c\). Az \(\displaystyle ABC\) és a \(\displaystyle PBC\) háromszög \(\displaystyle BC\) oldala közös, az ehhez tartozó magasságok párhuzamosak, arányuk a párhuzamos szelők tétele miatt \(\displaystyle A_1A:A_1P\). Ezért

\(\displaystyle \frac{A_1A}{A_1P} = \frac{T_{ABC}}{T_{PBC}}. \)

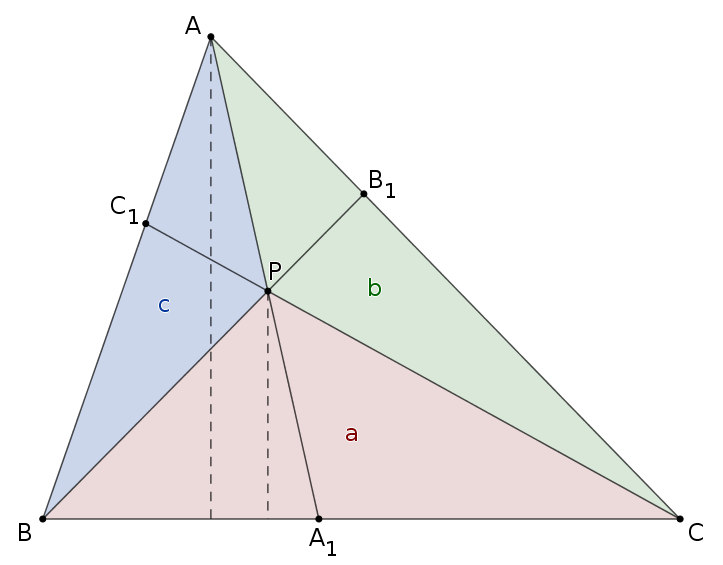
Figyelembe véve, hogy \(\displaystyle A_1A=A_1P+AP\), \(\displaystyle T_{PBC}=a\) és \(\displaystyle T_{ABC}=a+b+c\),

\(\displaystyle \frac{A_1P+AP}{A_1P} = \frac{a+b+c}{a}; \)

mindkét oldalból \(\displaystyle 1\)-et kivonva

\(\displaystyle \frac{AP}{A_1P} = \frac{b+c}{a}. \)

A betűzés ciklikus cseréjével, ugyanígy kapjuk, hogy

\(\displaystyle \frac{BP}{B_1P} = \frac{c+a}{b} \quad\text{és}\quad \frac{CP}{C_1P} = \frac{a+b}{c}. \)

A kapott azonosságokat behelyettesítve, a feladat állítása a következő egyenlőtlenséggel ekvivalens:

Az (1) egyenlőtlenséget úgy igazoljuk, hogy a baloldalon mindhárom tört számlálóját alulról becsüljük a számtani és mértani közepek közötti egyenlőtlenséggel:

\(\displaystyle \frac{b+c}{a} \cdot \frac{c+a}{b} \cdot \frac{a+b}{c} \ge \frac{2\sqrt{bc}}{a} \cdot \frac{2\sqrt{ca}}{b} \cdot \frac{2\sqrt{ab}}{c} = 8. \)

A becslésünkben akkor áll egyenlőség, ha mindhárom esetben egymással egyenlő számok közepeit hasonlítjuk össze, vagyis ha \(\displaystyle a=b=c\). Szintén a területek arányaiból látjuk, hogy

\(\displaystyle \frac{a}{b} = \frac{T_{PBC}}{T_{PCA}} = \frac{BC_1}{C_1A}; \)

az \(\displaystyle a=b\) feltétel tehát akkor teljesül, ha \(\displaystyle C_1\) az \(\displaystyle AB\) oldal felezőpontja. Ugyanígy, \(\displaystyle a=c\) és \(\displaystyle b=c\) akkor teljesül, ha \(\displaystyle B_1\) az \(\displaystyle AC\), illetve ha \(\displaystyle A_1\) a \(\displaystyle BC\) oldal felezőpontja. A feladat állításában tehát akkor áll egyenlőség, ha \(\displaystyle P\) az \(\displaystyle ABC\) háromszög súlypontja.

Statistics:

67 students sent a solution.
4 points:	62 students.
2 points:	1 student.
1 point:	3 students.
0 point:	1 student.

Problems in Mathematics of KöMaL, November 2019