Problem B. 5060. (November 2019)

B. 5060. In the plane \(\displaystyle \Sigma\), given a circle \(\displaystyle k\) and a point \(\displaystyle P\) in its interior, not coinciding with the center of \(\displaystyle k\). Call a point \(\displaystyle O\) of space, not lying on \(\displaystyle \Sigma\), a proper projection center if there exists a plane \(\displaystyle \Sigma'\), not passing through \(\displaystyle O\), such that, by projecting the points of \(\displaystyle \Sigma\) from \(\displaystyle O\) to \(\displaystyle \Sigma'\), the projection of \(\displaystyle k\) is also a circle, and its center is the projection of \(\displaystyle P\). Show that the proper projection centers lie on a circle.

(6 pont)

Deadline expired on December 10, 2019.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Tekintsünk egy tetszőleges \(\displaystyle O\) pontot, amely jó vetítő középpont, és tegyük fel, hogy a \(\displaystyle k\) kör az \(\displaystyle O\) pontból egy \(\displaystyle k'\) körbe vetíthető úgy, hogy \(\displaystyle K\) képe, \(\displaystyle K'\) éppen \(\displaystyle k'\) középpontja. Vetítsük \(\displaystyle O\)-ból tovább \(\displaystyle k'\)-t abba a síkba, amely átmegy a \(\displaystyle K\) ponton, és párhuzamos \(\displaystyle k'\) síkjával; ez a harmadik kör legyen \(\displaystyle k_1\). A síkok párhuzamossága miatt \(\displaystyle k_1\) középpontja \(\displaystyle K\). A továbbiakban a \(\displaystyle k\) síkjában bármely \(\displaystyle X\) pontjának képeit a két vetítés során \(\displaystyle X'\)-vel, illetve \(\displaystyle X_1\)-gyel fogjuk jelölni, és csak az \(\displaystyle X\mapsto X_1\) megfeleltetést fogjuk vizsgálni; "az \(\displaystyle X\) pont képének" az \(\displaystyle X_1\) pontot fogjuk hívni.

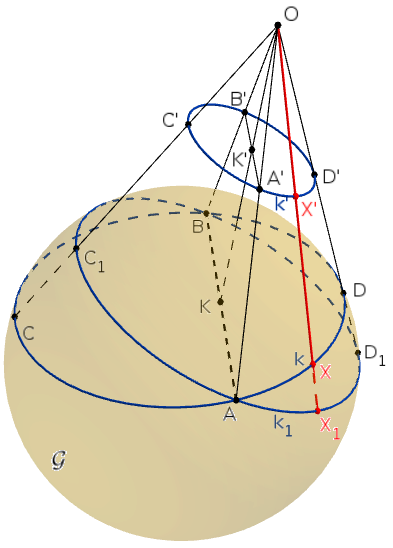
Vegyük észre, hogy \(\displaystyle k\) és \(\displaystyle k_1\) nem lehet ugyanaz a körvonal, és emiatt nem lehet ugyanabban a síkban sem, mert a \(\displaystyle K\) pont \(\displaystyle k_1\)-nek középpontja, \(\displaystyle k\)-nak pedig nem középpontja. Azok a pontok, amelyek önmaguk képei (az \(\displaystyle X\mapsto X_1\) megfeleltetés "fixpontjai"), a két kör síkjának közös pontjai, tehát egy egyenesen vannak. Egy konkrét fixpont a \(\displaystyle K\) pont a \(\displaystyle k\) kör belsejében, tehát a két sík metszésvolala elmetszi a \(\displaystyle k\) körvonalat is; a két metszéspontjuk legyen \(\displaystyle A\) és \(\displaystyle B\). Ekkor tehát \(\displaystyle A\) és \(\displaystyle B\) is fixpont, így \(\displaystyle A_1=A\) és \(\displaystyle B_1=B\) a \(\displaystyle k_1\) körön is rajta van. A \(\displaystyle k_1\) körben az \(\displaystyle AB\) húr átmérő, ezért \(\displaystyle K\) felezi az \(\displaystyle AB\) szakaszt. A \(\displaystyle k\) körben viszont legfeljebb egy olyan húr lehet, amelyet a \(\displaystyle K\) pont felez. Ezért az \(\displaystyle AB\) húr nem függ attól, hogy melyik \(\displaystyle O\) pontot választottuk.

Jelöljük a két körvonalra illeszkedő gömböt \(\displaystyle \mathcal{G}\)-vel. Bármely, az \(\displaystyle A\)-tól és \(\displaystyle B\)-től különböző \(\displaystyle X\) pontra \(\displaystyle OX\cdot OX_1\) az \(\displaystyle O\) pontnak a \(\displaystyle \mathcal{G}\)-re vonatkozó hatványa, állandó. Tehát az \(\displaystyle X\mapsto X_1\) megfeleltetés egy \(\displaystyle O\) pólusú inverzió. Az \(\displaystyle X\to A,B\) határátmenetekből látjuk, hogy \(\displaystyle OA^2=OA\cdot OA_1=OB\cdot OB_1=OB^2\), vagyis \(\displaystyle OA=OB\). Az \(\displaystyle O\) pont csak az \(\displaystyle AB\) szakasz felező merőleges síkjában lehet.

Legyen \(\displaystyle k_1\)-nek az \(\displaystyle AB\)-re merőleges átmérője \(\displaystyle CD\), ennek képe, \(\displaystyle C_1D_1\) a \(\displaystyle k_1\) körben átmérő. Mivel \(\displaystyle k\) és az \(\displaystyle AB\) húr rögzített, a \(\displaystyle CD\) húr sem függ az \(\displaystyle O\) ponttól. Legyen tehát \(\displaystyle C\) és \(\displaystyle D\) is rögzített; legyen \(\displaystyle KC=c\) és \(\displaystyle KD=d\). A vetítés és inverzió miatt \(\displaystyle O,C,C_1\), illetve \(\displaystyle O,D,D_1\) egy egyenesen van. Legyen \(\displaystyle CD_1\) és \(\displaystyle DC_1\) metszéspontja \(\displaystyle U\), a \(\displaystyle CD\) és az \(\displaystyle OU\) egyenes metszéspontja \(\displaystyle L\). Az inverzió miatt a \(\displaystyle C,D,C_1,D_1\) pontok egy körön vannak és \(\displaystyle KC_1=KD_1\); a \(\displaystyle K\) pontnak a \(\displaystyle CDC_1D_1\) körre vonatkozó hatványából kapjuk, hogy \(\displaystyle KC_1=KD_1=\sqrt{KC\cdot KD}=\sqrt{cd}\).

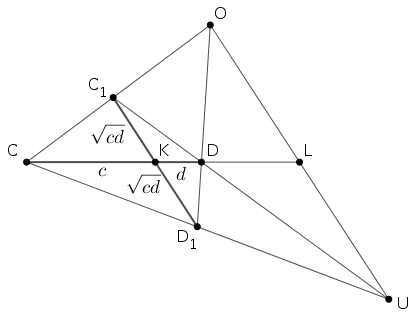
Számítsuk ki a \(\displaystyle \frac{C_1D}{DU}\) arányt úgy, hogy a Menelaosz-tételt felírjuk a \(\displaystyle C_1KD\) háromszögre és a \(\displaystyle CD_1U\) egyenesre:

Hasonlóan, ha a \(\displaystyle D_1DK\) háromszögre írjuk fel a Menelaosz-tételt, azt kapjuk, hogy \(\displaystyle \frac{D_1D}{DO} = \frac{c-d}{c+d}\). A \(\displaystyle C_1D_1D\) és az \(\displaystyle UDO\) hármszögek egy \(\displaystyle D\) középpontú, \(\displaystyle -\frac{c+d}{c-d}\) arányú nagyítással vihetők át egymásba. A \(\displaystyle K\) képe, az \(\displaystyle L\) pont, az \(\displaystyle OU\) szakasz felezőpontja, amit a \(\displaystyle C,D,K\) pontok egyértelműen meghatároznak, továbbá \(\displaystyle |LO|=\frac{c+d}{|c-d|}\cdot|KD_1|=\frac{c+d}{|c-d|}\sqrt{cd}\).

Azt kaptuk, hogy az \(\displaystyle AB\) szakasz és az \(\displaystyle L\) pont bármelyik jó vetítési középpont esetén ugyanaz, a vetítési középpont az \(\displaystyle AB\) szakasz felező merőleges síkjában van, egy \(\displaystyle L\) középpontú, \(\displaystyle \frac{c+d}{|c-d|}\sqrt{cd}\) sugarú körön.

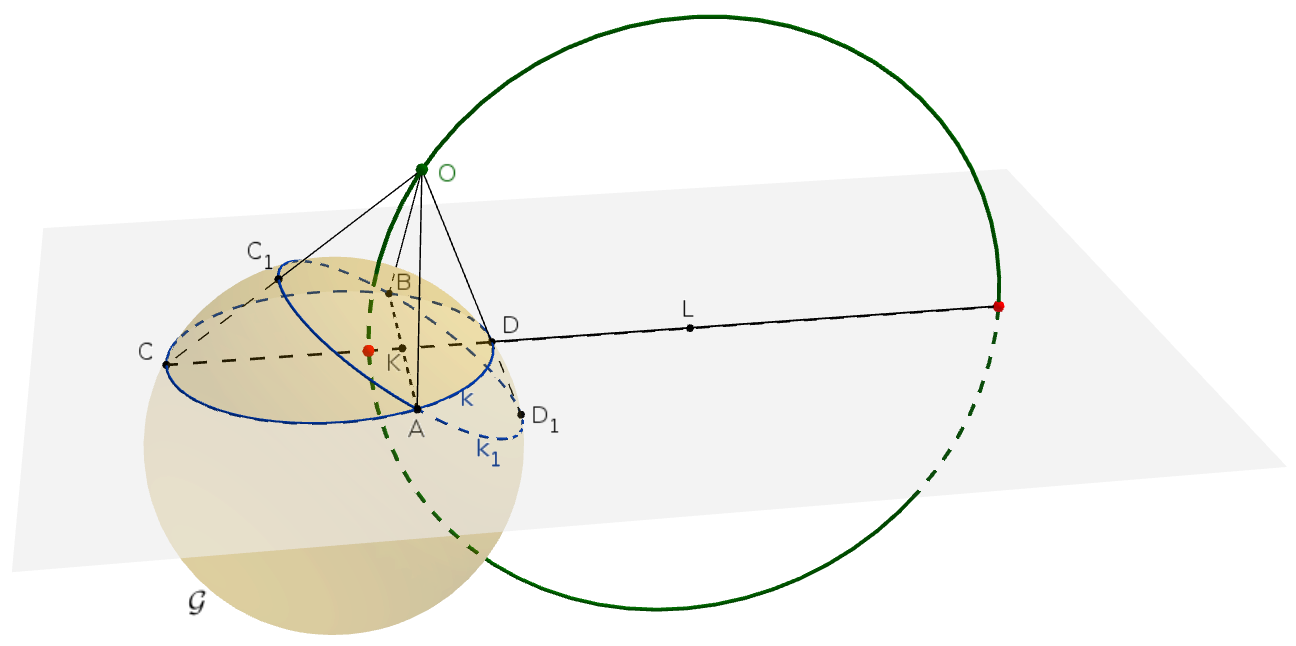
Megjegyzés. Könnyű meggondolni, hogy a kapott körnek két pontja a \(\displaystyle k\) kör síkjában van, ezért nem lehet vetítési középpont, de a körvonal többi pontja mind megfelelő.

Statistics:

8 students sent a solution.
6 points:	Beke Csongor.
5 points:	Fleiner Zsigmond.
4 points:	2 students.
3 points:	1 student.
0 point:	3 students.

Problems in Mathematics of KöMaL, November 2019