A B. 5087. feladat (2020. március)

B. 5087. Az \(\displaystyle ABCD\) négyzet egy belső \(\displaystyle P\) pontjának távolsága az \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle D\) csúcsoktól rendre \(\displaystyle 1\), \(\displaystyle \sqrt2\), illetve \(\displaystyle 2\). Számítsuk ki az \(\displaystyle APB\) szög nagyságát.

Javasolta: Bíró Bálint (Eger)

(4 pont)

A beküldési határidő 2020. április 14-én LEJÁRT.

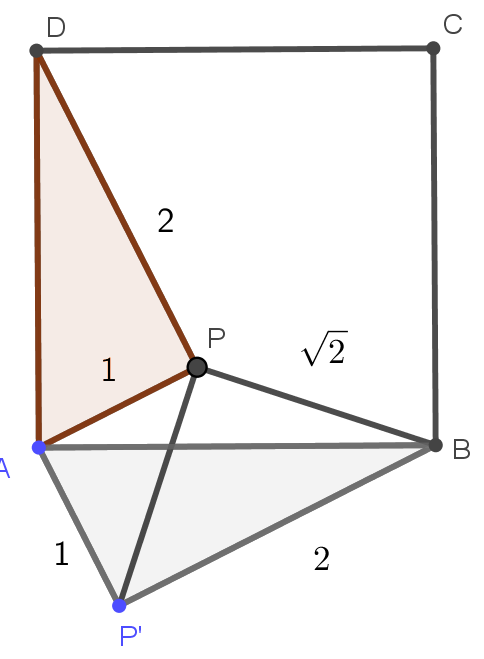
Megoldás. Forgassuk el az \(\displaystyle APD\) háromszöget az \(\displaystyle A\) pont körül \(\displaystyle 90^{\circ}\)-kal úgy, hogy a \(\displaystyle D\) pont a \(\displaystyle B\) pontba kerüljön, az ábra szerint. Legyen a \(\displaystyle P\) pont képe a \(\displaystyle P'\) pont. A \(\displaystyle PAP'\) háromszög egyenlő szárú derékszögű, így \(\displaystyle PP'=\sqrt{2}\), továbbá \(\displaystyle APP'\sphericalangle=45^{\circ}\). A \(\displaystyle P'PB\) háromszög oldalai \(\displaystyle \sqrt{2}, \sqrt{2}, 2\), ez a háromszög is egyenlő szárú és derékszögű, azaz \(\displaystyle P'PB\sphericalangle=90^{\circ}\). A keresett szög

\(\displaystyle APB\sphericalangle=APP'\sphericalangle+P'PB\sphericalangle=45^{\circ}+90^{\circ}=135^{\circ}.\)

A megoldás során azt is látjuk, hogy \(\displaystyle AP'B\sphericalangle=AP'P\sphericalangle+P'PB\sphericalangle=45^{\circ}+45^{\circ}=90^{\circ}\), tehát a négyzet oldala \(\displaystyle \sqrt{5}\) egység.

Statisztika:

89 dolgozat érkezett.
4 pontot kapott:	60 versenyző.
3 pontot kapott:	17 versenyző.
2 pontot kapott:	7 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	4 versenyző.

A KöMaL 2020. márciusi matematika feladatai