Problem B. 5087. (March 2020)

B. 5087. The distances of an interior point \(\displaystyle P\) of a square \(\displaystyle ABCD\) from the vertices \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle D\) are \(\displaystyle 1\), \(\displaystyle \sqrt2\,\), and \(\displaystyle 2\), respectively. Calculate the measure of the angle \(\displaystyle APB\).

Proposed by B. Bíró, Eger

(4 pont)

Deadline expired on April 14, 2020.

Sorry, the solution is available only in Hungarian. Google translation

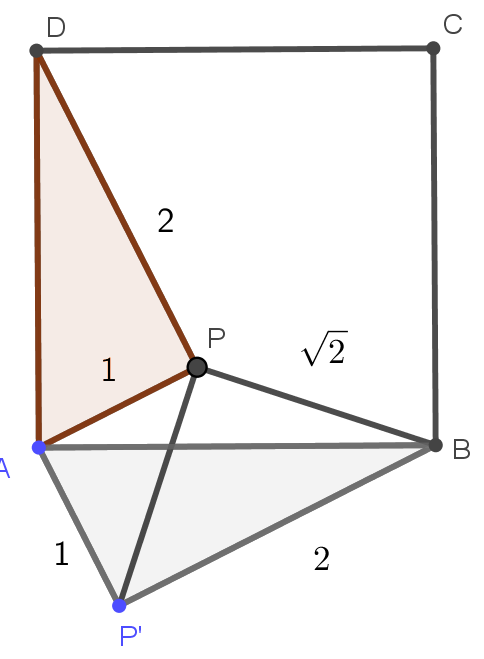
Megoldás. Forgassuk el az \(\displaystyle APD\) háromszöget az \(\displaystyle A\) pont körül \(\displaystyle 90^{\circ}\)-kal úgy, hogy a \(\displaystyle D\) pont a \(\displaystyle B\) pontba kerüljön, az ábra szerint. Legyen a \(\displaystyle P\) pont képe a \(\displaystyle P'\) pont. A \(\displaystyle PAP'\) háromszög egyenlő szárú derékszögű, így \(\displaystyle PP'=\sqrt{2}\), továbbá \(\displaystyle APP'\sphericalangle=45^{\circ}\). A \(\displaystyle P'PB\) háromszög oldalai \(\displaystyle \sqrt{2}, \sqrt{2}, 2\), ez a háromszög is egyenlő szárú és derékszögű, azaz \(\displaystyle P'PB\sphericalangle=90^{\circ}\). A keresett szög

\(\displaystyle APB\sphericalangle=APP'\sphericalangle+P'PB\sphericalangle=45^{\circ}+90^{\circ}=135^{\circ}.\)

A megoldás során azt is látjuk, hogy \(\displaystyle AP'B\sphericalangle=AP'P\sphericalangle+P'PB\sphericalangle=45^{\circ}+45^{\circ}=90^{\circ}\), tehát a négyzet oldala \(\displaystyle \sqrt{5}\) egység.

Statistics:

89 students sent a solution.
4 points:	60 students.
3 points:	17 students.
2 points:	7 students.
1 point:	1 student.
0 point:	4 students.

Problems in Mathematics of KöMaL, March 2020