A B. 5089. feladat (2020. március)

B. 5089. Egy tetraéder két kitérő éle egymásra merőleges, hosszuk 12 és 13, egyeneseik távolsága 14 egység. Határozzuk meg a tetraéder térfogatát.

(3 pont)

A beküldési határidő 2020. április 14-én LEJÁRT.

Megoldás. Legyenek a kitérő élek \(\displaystyle AC=12\) és \(\displaystyle BD=13\). Írjunk a tetraéder köré \(\displaystyle AB'CD'A'BC'D\) paralelepipedont az ábra szerint (lásd Geometriai feladatok gyűjteménye I. 2069. és 2071. feladatokat).

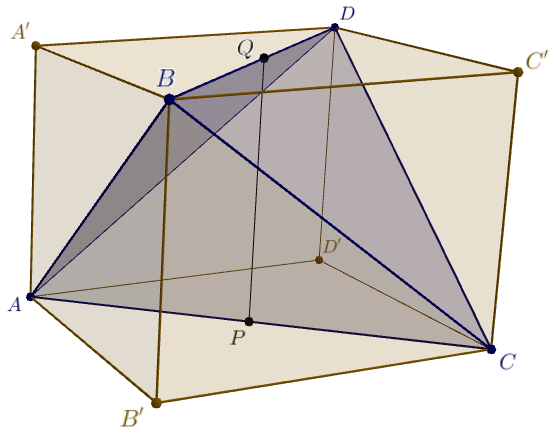
Mivel \(\displaystyle AC\perp BD\) a feltevés szerint, így \(\displaystyle AC\perp B'D'\) is teljesül, ezért az \(\displaystyle AB'CD'\) paralelogramma rombusz, területe pedig átlói szorzatának fele: \(\displaystyle 12\cdot 13/2=78\). Mivel az \(\displaystyle AC\) és \(\displaystyle BD\) egyenesek normáltranszverzálisa az \(\displaystyle AB'CD'\) és \(\displaystyle A'BC'D\) lapok mindegyikére merőleges, így az \(\displaystyle AB'CD'A'BC'D\) paralelepipedon \(\displaystyle AB'CD'\) lapjához tartozó magassága éppen az \(\displaystyle AC\) és \(\displaystyle BD\) egyenesek távolsága, azaz \(\displaystyle 14\). Az eddigiekből következik, hogy az \(\displaystyle AB'CD'A'BC'D\) paralelepipedon térfogata \(\displaystyle 78\cdot 14=1092\).

A Geometriai feladatok gyűjteménye I. 2083. feladata szerint az \(\displaystyle ABCD\) tetraéder térfogata az \(\displaystyle AB'CD'A'BC'D\) paralelepipedon térfogatának harmada, azaz \(\displaystyle 1092/3=364\).

Megjegyzés. A tetraéder szemközti élegyeneseinek távolsága jól kezelhető az élvektorok vektoriális és vegyes szorzataival. Lásd például ITT.

Statisztika:

67 dolgozat érkezett.
3 pontot kapott:	Bán-Szabó Áron, Farkas 512 Izabella, Fekete Richárd, Hervay Bence, Jánosik Áron, Kelemen Anna, Kercsó-Molnár Anita, Kerekes Boldizsár, Kovács Alex, Mohay Lili Veronika, Sándor Péter, Tiderenczl Dániel, Tóth 057 Bálint, Wiener Anna.
2 pontot kapott:	Andó Viola, Arató Zita, Balogh Ádám Péter, Beinschroth Ninett, Biró 424 Ádám, Csizmadia Miklós, Csonka Illés, Czett Mátyás, Feczkó Nóra, Gábriel Tamás, Halász Henrik, Jánosik Máté, Koleszár Domonkos, Koszta Benedek, Kovács Móric, Laki Anna, Lovas Márton, Mácsai Dániel, Molnár-Szabó Vilmos, Nádor Benedek, Nagy 551 Levente, Országh Júlia, Osztényi József, Páhán Anita Dalma, Seres-Szabó Márton, Somogyi Dalma, Szakács Ábel, Terjék András József, Török Mátyás, Trombitás Karolina Sarolta, Varga Boldizsár, Zempléni Lilla.
1 pontot kapott:	17 versenyző.
0 pontot kapott:	4 versenyző.

A KöMaL 2020. márciusi matematika feladatai