 |
A B. 5093. feladat (2020. március) |
B. 5093. Két egybevágó szabályos ötszög közös része egy tízszög, amelynek oldalai rendre \(\displaystyle a_1, a_2, \ldots, a_{10}\). Igazoljuk, hogy
\(\displaystyle a_1a_3+a_3a_5+a_5a_7+a_7a_9+a_9a_1 = a_2a_4+a_4a_6+a_6a_8+a_8a_{10}+a_{10}a_2. \)
(6 pont)
A beküldési határidő 2020. április 14-én LEJÁRT.
1. megoldás. Betűzzük a két ötszög csúcsait, oldalaik metszéspontjait és az oldal darabok hosszát az ábra szerint. Ezeket ciklikusan indexeljük, tehát például \(\displaystyle A_{11}=A_1\) vagy \(\displaystyle b_0=b_{10}\). A különböző sokszögek területét \(\displaystyle T(...)\)-vel fogjuk jelölni.
Vegyük észre, hogy minden \(\displaystyle i\)-re az \(\displaystyle A_iB_{i-1}B_i\) és \(\displaystyle A_{i+1}B_{i+1}B_i\) háromszögek hasonlók, mert a szögeik megegyeznek; ezért az \(\displaystyle A_1B_{10}B_1\), \(\displaystyle A_2B_2B_1\), \(\displaystyle A_3B_2B_2\), ... \(\displaystyle A_{10}B_{10}B_9\) háromszögek mind hasonlók.

A feladat megoldásához három, az \(\displaystyle a_1,\ldots,a_{10}\) távolságokra mindig érvényes azonosságot fogunk felírni.
1. Fejezzük ki a két ötszög kerületét az \(\displaystyle a_1,\ldots,a_{10}\) oldalakkal. A tíz kicsi háromszög hasonlósága miatt vannak olyan pozitív \(\displaystyle p,q\) valós számok, hogy \(\displaystyle b_i=p\cdot a_i\) és \(\displaystyle c_i=q\cdot a_i\) mindegyik \(\displaystyle i\) indexre; abból, hogy \(\displaystyle b_i+c_i>a_i\), következik, hogy \(\displaystyle p+q>1\). Ezeket behelyettesítve, a két ötszög kerülete
$$\begin{gather*} A_1A_3+A_3A_5+A_5A_7+A_7A_9+A_9A_1 = \\ = (c_1+a_2+b_3)+(c_3+a_4+b_5)+(c_5+a_6+b_7) +(c_7+a_8+b_9)+(c_9+a_{10}+b_1) = \\ = (a_2+a_4+a_6+a_8+a_{10})+(b_1+b_3+b_5+b_7+b_9)+(c_1+c_3+c_5+c_7+c_9) = \\ = (a_2+a_4+a_6+a_8+a_{10})+(p+q)(a_1+a_3+a_5+a_7+a_9), \end{gather*}$$és hasonlóan
\(\displaystyle A_2A_4+A_4A_6+A_6A_8+A_8A_{10}+A_{10}A_2 = (a_1+a_3+a_5+a_7+a_9)+(p+q)(a_2+a_4+a_6+a_8+a_{10}). \)
A két ötszög kerülete egyenlő, ezért
$$\begin{gather*} (a_2+a_4+a_6+a_8+a_{10})+(p+q)(a_1+a_3+a_5+a_7+a_9) = \qquad\qquad\qquad \\ \qquad\qquad\qquad = (a_1+a_3+a_5+a_7+a_9)+(p+q)(a_2+a_4+a_6+a_8+a_{10}) \\ (p+q-1)(a_1+a_3+a_5+a_7+a_9) = (p+q-1)(a_2+a_4+a_6+a_8+a_{10}) \\ a_1+a_3+a_5+a_7+a_9 = a_2+a_4+a_6+a_8+a_{10}. \tag{S} \end{gather*}$$2. Írjuk fel a két ötszög területét is. A hasonló háromszögek területei az oldalak négyzetével arányosak, ezért egy alkalmas pozitív \(\displaystyle r\) számmal az \(\displaystyle A_iB_{i-1}B_i\) háromszög területe \(\displaystyle r\cdot a_i^2\). Így
$$\begin{gather*} T(A_1A_3A_5A_7A_9) = T(B_1B_2\ldots B_{10}) + T(A_1B_{10}B_1)+T(A_3B_2B_3)+\ldots+T(A_9B_8B_9) = \\ = T(B_1B_2\ldots B_{10}) + r(a_1^2+a_3^2+a_5^2+a_7^2+a_9^2) \end{gather*}$$és ugyanígy
\(\displaystyle T(A_2A_4A_6A_8A_{10}) = T(B_1B_2\ldots B_{10}) + r(a_2^2+a_4^2+a_6^2+a_8^2+a_{10}^2); \)
a két ötszög területe is ugyanakkora, tehát
$$\begin{gather*} a_1^2+a_3^2+a_5^2+a_7^2+a_9^2 = a_2^2+a_4^2+a_6^2+a_8^2+a_{10}^2 \tag{N}. \end{gather*}$$3. A \(\displaystyle B_1B_2\ldots B_{10}\) tízszög oldalvektorainak összege a nullvektor, emiatt
\(\displaystyle \overrightarrow{B_{10}B_1}+\overrightarrow{B_2B_3}+ \overrightarrow{B_4B_5}+\overrightarrow{B_6B_7}+\overrightarrow{B_8B_9} = -\Big(\overrightarrow{B_1B_2}+\overrightarrow{B_3B_4}+ \overrightarrow{B_5B_6}+\overrightarrow{B_7B_8}+\overrightarrow{B_9B_{10}}\Big); \)
(skalárisan) négyzetre emelve
$$\begin{gather*} \Big(\overrightarrow{B_{10}B_1}+\overrightarrow{B_2B_3}+\overrightarrow{B_4B_5}+ \overrightarrow{B_6B_7}+\overrightarrow{B_8B_9}\Big)^2 = \Big(\overrightarrow{B_1B_2}+\overrightarrow{B_3B_4}+\overrightarrow{B_5B_6}+ \overrightarrow{B_7B_8}+\overrightarrow{B_9B_{10}}\Big)^2. \end{gather*}$$Mindegyik \(\displaystyle i\) indexre \(\displaystyle \Big(\overrightarrow{B_{i-1}B_i}\Big)^2=a_i^2\). A \(\displaystyle \overrightarrow{B_{i-1}B_i}\) és \(\displaystyle \overrightarrow{B_{i+1}B_{i+2}}\) vektorok valamelyik ötszög szomszédos oldalain vannak, ezért \(\displaystyle 72^\circ\)-os szöget zárnak be; a skaláris szorzatuk tehát \(\displaystyle a_ia_{i+2}\cos72^\circ\). Ugyanígy, a \(\displaystyle \overrightarrow{B_{i-1}B_i}\) és \(\displaystyle \overrightarrow{B_{i+3}B_{i+4}}\) vektorok a megfelelő ötszög másodszomszédos oldalain vannak, a bezárt szögük \(\displaystyle 144^\circ\), tehát a skaláris szorzatuk \(\displaystyle a_ia_{i+4}\cos144^\circ\). A fenti négyzeteket kibontva,
$$\begin{gather*} (a_1^2+a_3^2+\ldots+a_9^2) +(a_1a_3+a_3a_5+\ldots+a_9a_1)\cdot 2\cos72^\circ +\qquad\qquad\qquad\qquad\\\qquad\qquad\qquad\qquad+ (a_1a_5+a_3a_7+\ldots+a_7a_1)\cdot 2\cos144^\circ =\qquad\\ \qquad= (a_2^2+a_4^2+\ldots+a_{10}^2) +(a_2a_4+a_4a_6+\ldots+a_{10}a_2)\cdot 2\cos72^\circ +\qquad\qquad\qquad\qquad\\\qquad\qquad\qquad\qquad+ (a_2a_6+a_4a_8+\ldots+a_8a_2)\cdot 2\cos144^\circ. \tag{V} \end{gather*}$$4. Ezek után a feladat állítását úgy igazoljuk, hogy felírjuk (S) négyzetének és az (N) és (V) azonosságoknak egy lineáris kombinációját úgy, hogy kiessenek az \(\displaystyle a_i^2\) és az \(\displaystyle a_ia_{i+4}\) alakú tagok. Az (S), (N), (V) bal oldalaival számolva
$$\begin{gather*} (\textrm{V})-\cos144^\circ\cdot(\textrm{S})^2 -\big(1-\cos144^\circ\big)\cdot(\textrm{N}) = \\ = \Big((a_1^2+\ldots+a_9^2)+(a_1a_3+\ldots+a_9a_1)\cdot2\cos72^\circ+(a_1a_5+\ldots+a_7a_1)\cdot2\cos144^\circ\Big) - \qquad \\ \qquad -\cos144^\circ\cdot\Big(a_1+\ldots+a_9\Big)^2 -\big(1-\cos144^\circ\big)\cdot\Big(a_1^2+a_3^2+\ldots+a_9^2\Big) = \\ = 2\big(\cos72^\circ-\cos144^\circ\big)\cdot \Big(a_1a_3+a_3a_5+a_5a_7+a_7a_9+a_9a_1\Big). \end{gather*}$$A jobb oldalakkal számolva ugyanezt kapjuk a páros indexekkel, tehát
\(\displaystyle 2\big(\cos72^\circ-\cos144^\circ\big)\cdot\Big(a_1a_3+\ldots+a_9a_1\Big) = 2\big(\cos72^\circ-\cos144^\circ\big)\cdot\Big(a_2a_4+\ldots+a_{10}a_2\Big). \)
Az \(\displaystyle 2(\cos72^\circ-\cos144^\circ)\) együttható nem nulla, tehát oszthatunk vele, és megkapjuk a bizonyítandó állítást:
\(\displaystyle a_1a_3+a_3a_5+a_5a_7+a_7a_9+a_9a_1 = a_2a_4+a_4a_6+a_6a_8+a_8a_{10}+a_{10}a_2. \)
2. megoldás (vázlat). Az ötszögek oldalait válasszuk egségnyinek. Rögzítsük az egyik, az \(\displaystyle A_1A_3A_5A_7A_9\) ötszöget, a középpontját jelölje \(\displaystyle O\), és rögzítsük a második \(\displaystyle n\)-szög oldalainak irányát; a második ötszög középpontja legyen az \(\displaystyle X=(x,y)\) változó pont. A második ötszög csúcsai az \(\displaystyle X\) függvényei, jelölje ezeket \(\displaystyle A_2(X),A_4(X),A_6(X),A_8(X),A_{10}(X)\). Az \(\displaystyle A_{k-1}A_{k+1}\) és \(\displaystyle A_kA_{k+2}\) egyenesek metszéspontja legyen \(\displaystyle B_k(X)\); a keletkező tízszög oldalainak előjeles hossza \(\displaystyle a_k(X)=\overrightarrow{B_{k-1}B_{k}}\cdot\overrightarrow{A_{k-1}A_{k+1}}\). Ha a \(\displaystyle B_1B_2\ldots B_{10}\) töröttvonal egy konvex tízszöget határol, akkor az \(\displaystyle a_k\) számok mind azonos előjelűek. Azt fogjuk igazolni, hogy
$$\begin{gather*} \Big(a_1(X)a_3(X)+\ldots+a_9(X)a_1(X)\Big)- \Big(a_2(X)a_4(X)+\ldots+a_{10}(X)a_2(X)\Big) =0. \tag{A} \end{gather*}$$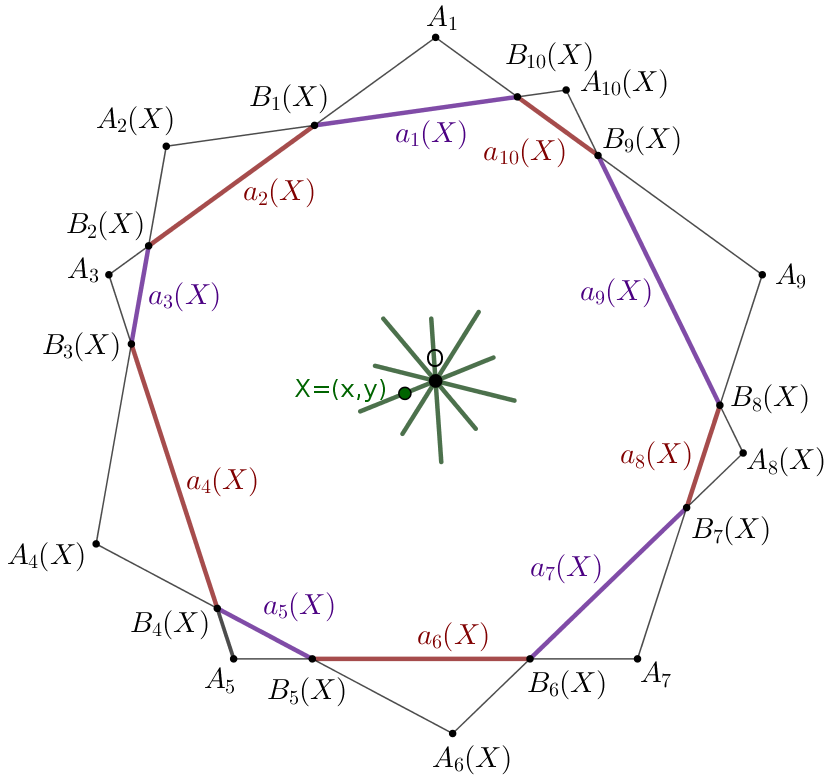
Az \(\displaystyle A_k(X)\), \(\displaystyle B_k(X)\) pontok koordinátái és az \(\displaystyle a_k(X)\) előjeles távolságok mind az \(\displaystyle x,y\) koordináták lineáris függvényei, ezért (A) baloldalán egy legfeljebb másodfokú kifejezés áll.
Ha \(\displaystyle OX\) merőleges az \(\displaystyle A_1A_3\) és \(\displaystyle A_2A_{10}\) irányok szögfelezőjére (amelynek iránya nem függ az \(\displaystyle X\) választásától), akkor a \(\displaystyle B_1B_2\ldots B_{10}\) töröttvonal szimmetrikus a \(\displaystyle B_1B_6\) egyenesre: \(\displaystyle a_1=a_2\), \(\displaystyle a_3=a_{10}\), \(\displaystyle a_5=a_8\), \(\displaystyle a_7=a_6\) és \(\displaystyle a_9=a_4\), emiatt (A) biztosan teljesül. Ugyanez igaz akkor, ha \(\displaystyle OX\) merőleges \(\displaystyle A_3A_5\) és \(\displaystyle A_4A_2\), \(\displaystyle A_5A_7\) és \(\displaystyle A_6A_4\) \(\displaystyle A_7A_9\) és \(\displaystyle A_8A_6\) vagy \(\displaystyle A_9A_1\) és \(\displaystyle A_{10}A_7\) szögfelezőjére; ezzel már öt különböző irányú egyenest mutattunk, amelyen (A) teljesül.
Ha (A) baloldala pontosan elsőfokú, akkor (A) egyetlen egyenesen teljesülhet. Ha pedig (A) pontosan másodfokú, akkor egy (esetleg elfajuló) kúpszelet egyenlete; egyik esetben teljesülhet kettőnél több egyenesen.
Az az egy eset maradt tehát, hogy (A) azonosság, akkor viszont az \(\displaystyle X\) bármely választása esetén teljesül.
Megjegyzés. A második megoldás mutatja, hogy az állítás általánosabban is igaz, ötszögek helyett szabályos \(\displaystyle n\)-szögekkel és másodfokú helyett magasabb fokú kifejezésekkel is.
Statisztika:
15 dolgozat érkezett. 6 pontot kapott: Bán-Szabó Áron, Baski Bence, Beke Csongor, Fekete Richárd, Fleiner Zsigmond, Füredi Erik Benjámin, Kovács 129 Tamás, Lengyel Ádám. 4 pontot kapott: 2 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2020. márciusi matematika feladatai

