 |
A B. 5096. feladat (2020. április) |
B. 5096. Az \(\displaystyle ABC\) egységnyi oldalú szabályos háromszögben legyen \(\displaystyle P\) a beírható körvonal tetszőleges pontja. Jelölje a \(\displaystyle P\) pont merőleges vetületét a \(\displaystyle BC\), \(\displaystyle AC\) és \(\displaystyle AB\) oldalakra rendre \(\displaystyle D\), \(\displaystyle E\), illetve \(\displaystyle F\). Igazoljuk, hogy a \(\displaystyle DEF\) háromszög területe \(\displaystyle P\) választásától független állandó.
(4 pont)
A beküldési határidő 2020. május 11-én LEJÁRT.
Megoldás. Használjuk az ábra jelöléseit, legyenek az oldalvektorok \(\displaystyle \overrightarrow{AB}=\mathbf c\), \(\displaystyle \overrightarrow{BC}=\mathbf a\) és \(\displaystyle \overrightarrow{CA}=\mathbf b\); nyilván \(\displaystyle |\mathbf a|=|\mathbf b| = |\mathbf c|= 1\). Legyen továbbá \(\displaystyle \overrightarrow {OP}=\mathbf p\), ahol \(\displaystyle |\mathbf p|= r=1/(2\sqrt 3)\) a beírt kör sugara.
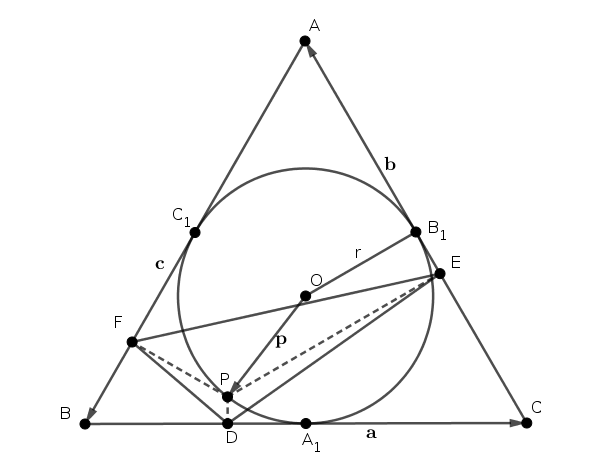
A skaláris szorzat geometriai jelentése szerint az \(\displaystyle \mathbf a \mathbf p\) skaláris szorzat éppen az \(\displaystyle A_1D\) szakasz előjeles hossza, így \(\displaystyle BD=BA_1\pm A_1D=1/2+\mathbf a \mathbf p\). Hasonlóan látható, hogy \(\displaystyle DC=1/2-\mathbf a \mathbf p\); \(\displaystyle CE=1/2+\mathbf b \mathbf p\); \(\displaystyle EA=1/2-\mathbf b \mathbf p\); \(\displaystyle AF=1/2+\mathbf c \mathbf p\) és \(\displaystyle FB=1/2-\mathbf c \mathbf p\).
A \(\displaystyle DEF\) háromszög területét megkapjuk, ha az \(\displaystyle FBD\), \(\displaystyle DCE\) és \(\displaystyle EAF\) háromszögek területeinek összegét levonjuk az \(\displaystyle ABC\) területéből.
$$\begin{align*} & T_{BDF}+T_{DCE}+T_{EAF}=\frac{BD \cdot BF\cdot \sin 60^\circ}{2}+\frac{CD \cdot CE\cdot \sin 60^\circ}{2}+\frac{AE \cdot AF\cdot \sin 60^\circ}{2}=\\ & = \frac{\sqrt 3}{4}\left [(1/2+\mathbf a \mathbf p)(1/2-\mathbf c \mathbf p)+(1/2-\mathbf a \mathbf p)(1/2+\mathbf b \mathbf p)+(1/2-\mathbf b \mathbf p)(1/2+\mathbf c \mathbf p) \right ]=\\ & =\frac{\sqrt 3}{4}\left [\frac 34 - \left ((\mathbf a \mathbf p)(\mathbf b \mathbf p)+(\mathbf a \mathbf p)(\mathbf c \mathbf p)+(\mathbf b \mathbf p)(\mathbf c \mathbf p) \right )\right ] \end{align*}$$Ha \(\displaystyle \mathbf p\) és \(\displaystyle \mathbf a\) bezárt szöge \(\displaystyle \theta\), akkor \(\displaystyle \mathbf p\) és \(\displaystyle \mathbf b\) szöge \(\displaystyle \theta +120^\circ\), valamint \(\displaystyle \mathbf p\) és \(\displaystyle \mathbf c\) szöge \(\displaystyle \theta +240^\circ\), hiszen az \(\displaystyle \mathbf a\), \(\displaystyle \mathbf b\) és \(\displaystyle \mathbf c\) vektorok egymás \(\displaystyle \pm 120^\circ\)-os elforgatottjai. Így
$$\begin{align*} &(\mathbf a \mathbf p)(\mathbf b \mathbf p)+(\mathbf a \mathbf p)(\mathbf c \mathbf p)+(\mathbf b \mathbf p)(\mathbf c \mathbf p)=r^2(\cos \theta \cos (\theta +120^\circ)+\cos \theta \cos (\theta +240^\circ)+\cos (\theta +120^\circ)\cos (\theta +240^\circ))=\\ & =r^2\left [ \cos \theta\left ( \frac{-\cos \theta}{2}-\frac{\sqrt 3 \sin \theta}{2} \right )+ \cos \theta\left ( \frac{-\cos \theta}{2}+\frac{\sqrt 3 \sin \theta}{2} \right )+\left ( \frac{-\cos \theta}{2}-\frac{\sqrt 3 \sin \theta}{2} \right ) \left ( \frac{-\cos \theta}{2}+\frac{\sqrt 3 \sin \theta}{2} \right ) \right ]=\\ &= r^2\left (\frac {-3\cos^2 \theta}{4}+\frac {-3\sin^2 \theta}{4} \right )=\frac 1{12} \cdot \frac {-3}4=\frac {-1}{16}, \end{align*}$$ahol a számolásban felhasználtuk a koszinusz függvény addíciós formuláját. Innen pedig
\(\displaystyle T_{DEF}=T_{ABC}-(T_{BDF}+T_{DCE}+T_{EAF})=\frac{\sqrt 3}{4}-\frac{\sqrt 3}{4}\left (\frac 34+ \frac 1 {16} \right)=\frac{3\sqrt 3}{64},\)
ami valóban \(\displaystyle P\)-től független állandó.
Statisztika:
40 dolgozat érkezett. 4 pontot kapott: Balogh Ádám Péter, Bán-Szabó Áron, Baski Bence, Beinschroth Ninett, Beke Csongor, Czett Mátyás, Fekete Richárd, Fleiner Zsigmond, Füredi Erik Benjámin, Gábriel Tamás, Hervay Bence, Kerekes Boldizsár, Koszta Benedek, Nagy 551 Levente, Németh Márton, Seres-Szabó Márton, Somogyi Dalma, Szabó 991 Kornél, Terjék András József, Tiderenczl Dániel, Tóth 057 Bálint, Vakaris Klyvis. 3 pontot kapott: Al-Hag Máté Amin, Andó Viola, Fey Dávid, Hámori Janka, Laki Anna, Lengyel Ádám, Lovas Márton, Mácsai Dániel, Molnár Lehel, Móricz Benjámin, Osztényi József, Velich Nóra. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2020. áprilisi matematika feladatai

