 |
A B. 5099. feladat (2020. április) |
B. 5099. Az \(\displaystyle ABCD\) rombusz \(\displaystyle A\)-nál lévő szöge \(\displaystyle 60^\circ\). A rombuszba olyan ellipszist írtunk, amelynek tengelyei a rombusz átlói, továbbá az \(\displaystyle AB\) és \(\displaystyle AD\) oldalakat az \(\displaystyle A\)-hoz, a \(\displaystyle BC\) és \(\displaystyle CD\) oldalakat a \(\displaystyle C\)-hez közelebbi negyedelőpontjaikban érinti. Legyen \(\displaystyle P\) az ellipszis egy mozgó pontja. Metsszük el a rombusz mindkét középvonalát a \(\displaystyle P\) ponton keresztül húzott, a másik középvonallal párhuzamos egyenessel; jelöljük az így kapott metszéspontokat \(\displaystyle Q\)-val, illetve \(\displaystyle R\)-rel. Mutassuk meg, hogy a \(\displaystyle QR\) szakasz hossza nem függ a \(\displaystyle P\) pont helyzetétől.
(5 pont)
A beküldési határidő 2020. május 11-én LEJÁRT.
Megoldás. Válasszuk a koordináta-rendszert úgy, hogy a rombusz csúcsai \(\displaystyle A(-2\sqrt 3,0)\), \(\displaystyle B(0,-2)\), \(\displaystyle C(2\sqrt 3,0)\) és \(\displaystyle D(0,2)\) legyenek; s keressük az ellipszis egyenletét a szokásos \(\displaystyle x^2/a^2+y^2/b^2=1\) alakban. A \(\displaystyle CD\) oldal \(\displaystyle C\)-hez közelebbi negyedelőpontja \(\displaystyle N(3\sqrt 3/2, 1/2)\), továbbá a \(\displaystyle CD\) oldalegyenes egyenlete (tengelymetszetes alakban felírva) \(\displaystyle x/(2\sqrt 3)+y/2=1\). Jól ismert és számolással könnyen ellenőrizhető, hogy az ellipszishez az \(\displaystyle (x_0,y_0)\) pontjában húzott érintő egyenlete \(\displaystyle xx_0/a^2+yy_0/b^2=1\) (lásd Geometriai feladatok gyűjteménye II., 1001. feladat). Ez alapján az \(\displaystyle N\) pontban érintő \(\displaystyle CD\) egyenes egyenletére \(\displaystyle 3\sqrt 3x/2a^2+y/2b^2=1\) adódik, amiből \(\displaystyle a^2=9\) és \(\displaystyle b^2=1\), azaz az ellpiszis egyenlete \(\displaystyle x^2/9+y^2=1\). Szimmetriai okok miatt ez a többi érintési feltételt is teljesíti.
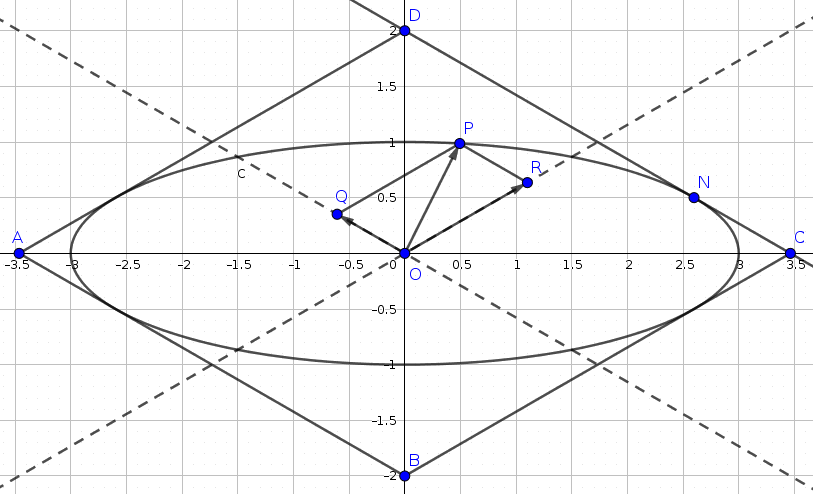
Legyen most \(\displaystyle P(\hat x, \hat y)\) az ellipszis egy tetszőleges pontja, a középvonalakon a megfelelő vetületei \(\displaystyle R\) és \(\displaystyle Q\) a feladat szövege szerint. Ekkor egyrészt alkalmas valós \(\displaystyle \lambda\) és \(\displaystyle \mu\) számokkal \(\displaystyle \overrightarrow{OR}=\lambda(\sqrt 3, 1)\) és \(\displaystyle \overrightarrow{OQ}=\mu(\sqrt 3, -1)\) (hiszen \(\displaystyle \overrightarrow{OR}\) és \(\displaystyle \overrightarrow{OQ}\) a középvonalakkal párhuzamos vektorok), másrészt \(\displaystyle ORPQ\) paralelogramma, így
\(\displaystyle \overrightarrow{OP}=\overrightarrow{OR}+\overrightarrow{OQ}=\lambda(\sqrt 3, 1) +\mu (\sqrt 3, -1),\)
azaz \(\displaystyle (\hat x, \hat y)=\overrightarrow{OP}=(\sqrt 3 (\lambda + \mu), \lambda-\mu)\). Végül
\(\displaystyle RQ^2=(\lambda \sqrt 3- \mu \sqrt 3)^2+(\lambda + \mu )^2=3\hat y^2+\frac {\hat x^2}3=3(\frac {\hat x^2} 9+ \hat y^2)=3,\)
azaz az \(\displaystyle RQ\) szakasz hossza valóban állandó. Ezt akartuk igazolni.
Statisztika:
28 dolgozat érkezett. 5 pontot kapott: Bán-Szabó Áron, Baski Bence, Beke Csongor, Czett Mátyás, Fekete Richárd, Fleiner Zsigmond, Füredi Erik Benjámin, Gábriel Tamás, Geretovszky Anna, Hervay Bence, Kovács 129 Tamás, Lengyel Ádám, Lovas Márton, Mácsai Dániel, Móra Márton Barnabás, Nádor Benedek, Nagy 551 Levente, Németh Márton, Osztényi József, Seres-Szabó Márton, Somogyi Dalma, Szabó 991 Kornél, Sztranyák Gabriella, Terjék András József, Tiderenczl Dániel, Velich Nóra. 4 pontot kapott: Kerekes Boldizsár. 3 pontot kapott: 1 versenyző.
A KöMaL 2020. áprilisi matematika feladatai

