Problem B. 5099. (April 2020)

B. 5099. The angle at vertex \(\displaystyle A\) of a rhombus \(\displaystyle ABCD\) is \(\displaystyle 60^\circ\). An ellipse is inscribed in the rhombus, with the axes lying along the diagonals of the rhombus. The points of tangency of the ellipse on sides divide the sides in a ratio \(\displaystyle 1:3\). On sides \(\displaystyle AB\) and \(\displaystyle AD\) it is the point closer to \(\displaystyle A\), and on sides \(\displaystyle BC\) and \(\displaystyle CD\) it is the point closer to \(\displaystyle C\). Let some point \(\displaystyle P\) move along the ellipse. Draw lines through \(\displaystyle P\), parallel to the midlines of the rhombus, and consider the intersections with the other midline. Let these point be \(\displaystyle Q\) and \(\displaystyle R\). Show that the length of the line segment \(\displaystyle QR\) is independent of the position of \(\displaystyle P\).

(5 pont)

Deadline expired on May 11, 2020.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Válasszuk a koordináta-rendszert úgy, hogy a rombusz csúcsai \(\displaystyle A(-2\sqrt 3,0)\), \(\displaystyle B(0,-2)\), \(\displaystyle C(2\sqrt 3,0)\) és \(\displaystyle D(0,2)\) legyenek; s keressük az ellipszis egyenletét a szokásos \(\displaystyle x^2/a^2+y^2/b^2=1\) alakban. A \(\displaystyle CD\) oldal \(\displaystyle C\)-hez közelebbi negyedelőpontja \(\displaystyle N(3\sqrt 3/2, 1/2)\), továbbá a \(\displaystyle CD\) oldalegyenes egyenlete (tengelymetszetes alakban felírva) \(\displaystyle x/(2\sqrt 3)+y/2=1\). Jól ismert és számolással könnyen ellenőrizhető, hogy az ellipszishez az \(\displaystyle (x_0,y_0)\) pontjában húzott érintő egyenlete \(\displaystyle xx_0/a^2+yy_0/b^2=1\) (lásd Geometriai feladatok gyűjteménye II., 1001. feladat). Ez alapján az \(\displaystyle N\) pontban érintő \(\displaystyle CD\) egyenes egyenletére \(\displaystyle 3\sqrt 3x/2a^2+y/2b^2=1\) adódik, amiből \(\displaystyle a^2=9\) és \(\displaystyle b^2=1\), azaz az ellpiszis egyenlete \(\displaystyle x^2/9+y^2=1\). Szimmetriai okok miatt ez a többi érintési feltételt is teljesíti.

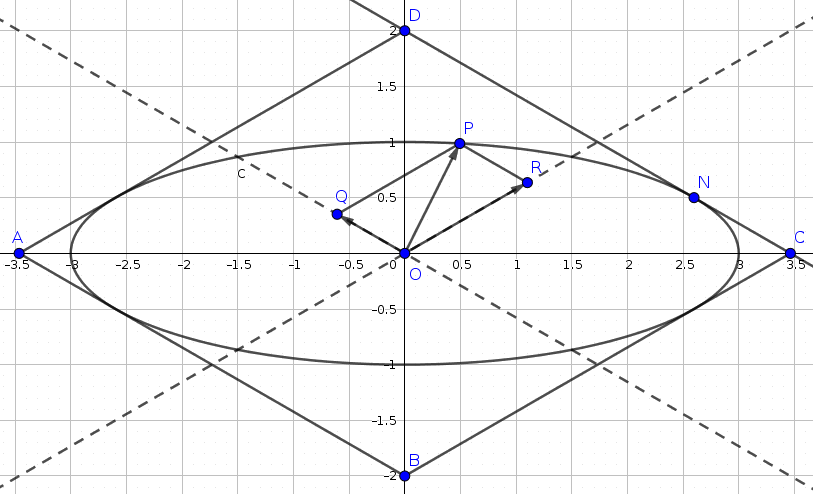
Legyen most \(\displaystyle P(\hat x, \hat y)\) az ellipszis egy tetszőleges pontja, a középvonalakon a megfelelő vetületei \(\displaystyle R\) és \(\displaystyle Q\) a feladat szövege szerint. Ekkor egyrészt alkalmas valós \(\displaystyle \lambda\) és \(\displaystyle \mu\) számokkal \(\displaystyle \overrightarrow{OR}=\lambda(\sqrt 3, 1)\) és \(\displaystyle \overrightarrow{OQ}=\mu(\sqrt 3, -1)\) (hiszen \(\displaystyle \overrightarrow{OR}\) és \(\displaystyle \overrightarrow{OQ}\) a középvonalakkal párhuzamos vektorok), másrészt \(\displaystyle ORPQ\) paralelogramma, így

\(\displaystyle \overrightarrow{OP}=\overrightarrow{OR}+\overrightarrow{OQ}=\lambda(\sqrt 3, 1) +\mu (\sqrt 3, -1),\)

azaz \(\displaystyle (\hat x, \hat y)=\overrightarrow{OP}=(\sqrt 3 (\lambda + \mu), \lambda-\mu)\). Végül

\(\displaystyle RQ^2=(\lambda \sqrt 3- \mu \sqrt 3)^2+(\lambda + \mu )^2=3\hat y^2+\frac {\hat x^2}3=3(\frac {\hat x^2} 9+ \hat y^2)=3,\)

azaz az \(\displaystyle RQ\) szakasz hossza valóban állandó. Ezt akartuk igazolni.

Statistics:

28 students sent a solution.
5 points:	Bán-Szabó Áron, Baski Bence, Beke Csongor, Czett Mátyás, Fekete Richárd, Fleiner Zsigmond, Füredi Erik Benjámin, Gábriel Tamás, Geretovszky Anna, Hervay Bence, Kovács 129 Tamás, Lengyel Ádám, Lovas Márton, Mácsai Dániel, Móra Márton Barnabás, Nádor Benedek, Nagy 551 Levente, Németh Márton, Osztényi József, Seres-Szabó Márton, Somogyi Dalma, Szabó 991 Kornél, Sztranyák Gabriella, Terjék András József, Tiderenczl Dániel, Velich Nóra.
4 points:	Kerekes Boldizsár.
3 points:	1 student.

Problems in Mathematics of KöMaL, April 2020