 |
A B. 5101. feladat (2020. április) |
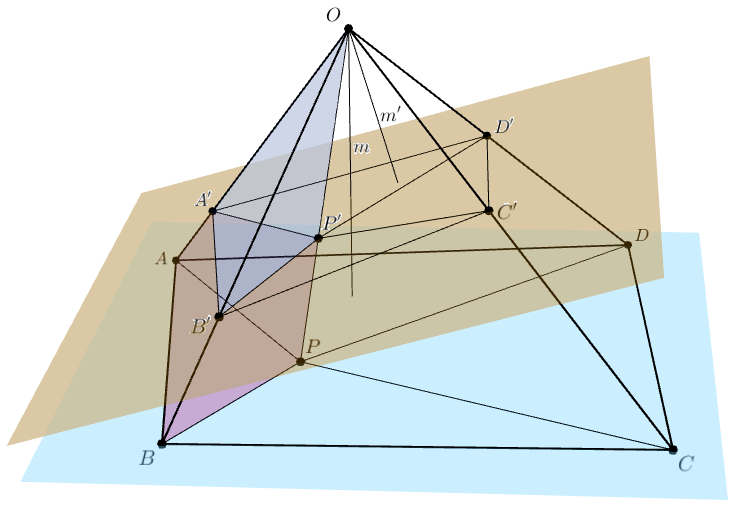
B. 5101. Adott egy \(\displaystyle ABCDO\) négyoldalú gúla, és az \(\displaystyle ABCD\) alaplap belsejében egy \(\displaystyle P\) pont. Egy \(\displaystyle O\)-ra nem illeszkedő sík az \(\displaystyle OA\), \(\displaystyle OB\), \(\displaystyle OC\), \(\displaystyle OD\) és \(\displaystyle OP\) egyeneseket rendre az \(\displaystyle A'\), \(\displaystyle B'\), \(\displaystyle C'\), \(\displaystyle D'\), illetve \(\displaystyle P'\) pontokban metszi. Igazoljuk, hogy
\(\displaystyle \frac{t_{PAB}\cdot t_{PCD}}{t_{PBC}\cdot t_{PDA}} = \frac{t_{P'A'B'}\cdot t_{P'C'D'}}{t_{P'B'C'}\cdot t_{P'D'A'}}. \)
(\(\displaystyle t_{XYZ}\) az \(\displaystyle XYZ\) háromszög területét jelöli.)
(6 pont)
A beküldési határidő 2020. május 11-én LEJÁRT.
Megoldás. A területek aránya helyett térfogatok arányával fogunk számolni.
Tetszőleges \(\displaystyle X,Y,Z,W\) pontok esetén jelölje \(\displaystyle v_{XYZW}\) az \(\displaystyle XYZW\) tetraéder térfogatát. Legyen a gúla magassága, vagyis az \(\displaystyle O\) pont távolsága az \(\displaystyle ABCD\) síktól \(\displaystyle m\), az \(\displaystyle A'BC'D'\) síktól pedig \(\displaystyle m'\), továbbá legyen \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), \(\displaystyle d\) és \(\displaystyle p\) az az öt valós szám, amelyre \(\displaystyle \overrightarrow{OA'} = a\cdot \overrightarrow{OA}\), \(\displaystyle \overrightarrow{OB'} = b\cdot \overrightarrow{OB}\), \(\displaystyle \overrightarrow{OC'} = c\cdot \overrightarrow{OC}\), \(\displaystyle \overrightarrow{OD'} = d\cdot \overrightarrow{OD}\), illetve \(\displaystyle \overrightarrow{OP'} = p\cdot \overrightarrow{OP}\). (A pontok és két sík elhelyezkedésétől függően az \(\displaystyle a,b,c,d,p\) számok pozitívak és negatívak is lehetnek.)
Írjuk fel az \(\displaystyle OPAB\) tetraéder térfogatát kétféleképpen, a \(\displaystyle PAB\) lap területével és az \(\displaystyle \overrightarrow{OP}\), \(\displaystyle \overrightarrow{OA}\), \(\displaystyle \overrightarrow{OB}\) élvektorok vegyes szorzatával:
$$\begin{gather*} v_{OPAB} = \frac13 \cdot t_{PAB}\cdot m = \frac16 \Big|\overrightarrow{OP}\cdot\big(\overrightarrow{OA}\times\overrightarrow{OB}\big)\Big|. \tag{1} \end{gather*}$$Hasonlóan írhatjuk fel az \(\displaystyle OP'A'B'\) tetraéder térfogatát kétféleképpen:
$$\begin{align*} v_{OP'A'B'} &= \frac13 \cdot t_{P'A'B'}\cdot m' = \frac16 \Big|\overrightarrow{OP'}\cdot\big(\overrightarrow{OA'}\times\overrightarrow{OB'}\big)\Big| =\\& = \frac16 \Big|(p\cdot \overrightarrow{OP})\cdot\big((a\cdot\overrightarrow{OA})\times(b\cdot\overrightarrow{OB})\big)\Big| = \frac{|pab|}6 \Big|\overrightarrow{OP}\cdot\big(\overrightarrow{OA}\times\overrightarrow{OB}\big)\Big| =\\& = |pab| \cdot v_{OPAB}. \tag{2} \end{align*}$$Az (1) és (2) összehasonlításából látjuk, hogy
\(\displaystyle \frac{t_{P'A'B'}}{t_{PAB}} = \frac{3v_{OP'A'B'}/m'}{3v_{OPAB}/m} = \frac{3|pab|\cdot v_{OPAB}/m'}{3v_{OPAB}/m} = \frac{|pab|\cdot m}{m'}. \)
Hasonlóan kaphatjuk, hogy
\(\displaystyle \frac{t_{P'B'C'}}{t_{PBC}} = \frac{|pbc|\cdot m}{m'}, \quad \frac{t_{P'C'D'}}{t_{PCD}} = \frac{|pcd|\cdot m}{m'}, \quad \text{és}\quad \frac{t_{P'D'A'}}{t_{PDA}} = \frac{|pda|\cdot m}{m'}. \)
Ezeket figyelembe véve, a bizonyítandó állítás két oldalának hányadosa:
$$\begin{align*} \frac{\text{baloldal}}{\text{jobboldal}} &= \frac{\dfrac{t_{PAB}\cdot t_{PCD}}{t_{PBC}\cdot t_{PDA}}}{\dfrac{t_{P'A'B'}\cdot t_{P'C'D'}}{t_{P'B'C'}\cdot t_{P'D'A'}}} = \frac{t_{PAB}}{t_{P'A'B'}} \cdot \frac{t_{PCD}}{t_{P'C'D'}} \cdot \frac{t_{P'B'C'}}{t_{PBC}} \cdot \frac{t_{P'D'A'}}{t_{PDA}} =\\ &= \frac{m'}{|pab|\cdot m} \cdot \frac{m'}{|pcd|\cdot m} \cdot \frac{|pbc|\cdot m}{m'} \cdot \frac{|pda|\cdot m}{m'} = 1. \end{align*}$$Statisztika:
12 dolgozat érkezett. 6 pontot kapott: Balogh Ádám Péter, Bán-Szabó Áron, Beke Csongor, Fleiner Zsigmond, Füredi Erik Benjámin, Kovács 129 Tamás, Seres-Szabó Márton, Szabó 991 Kornél, Sztranyák Gabriella, Tiderenczl Dániel. 5 pontot kapott: Velich Nóra. 1 pontot kapott: 1 versenyző.
A KöMaL 2020. áprilisi matematika feladatai

