 |
A B. 5102. feladat (2020. május) |
B. 5102. Adott a síkban \(\displaystyle n\) különböző pont, nem esik mind egy egyenesre. Mutassuk meg, hogy van olyan önmagát nem metsző, zárt töröttvonal, amelynek az adott pontok a csúcsai. (Egy töröttvonal csúcsánál lehet \(\displaystyle 180^{\circ}\)-os szög is.)
(3 pont)
A beküldési határidő 2020. június 10-én LEJÁRT.
Megoldás. Tekintsünk egy \(\displaystyle P\) pontot az adottak közül, és legyen a \(\displaystyle P\)-ből a többi adott pont felé induló összes félegyenes a \(\displaystyle P\) körüli pozitív körüljárás szerinti sorrendben \(\displaystyle f_1, f_2,\ldots, f_k\). (Egy félegyenesre több pont is illeszkedhet.) Jegyezzük meg, hogy a feltevés szerint \(\displaystyle k\ge 2\). Mivel az \(\displaystyle \angle(f_1,f_2)\), \(\displaystyle \angle(f_2,f_3)\), ..., \(\displaystyle \angle(f_k,f_1)\) irányított szögek összege éppen \(\displaystyle 360^\circ\), így közöttük legfeljebb egy konkáv szög lehet. Az indexelést választhatjuk úgy, hogy az \(\displaystyle \angle(f_k,f_1)\) legyen az egyik legnagyobb a felsorolt szögek közül, ekkor az \(\displaystyle \angle(f_1,f_2)\), \(\displaystyle \angle(f_2,f_3)\), ..., \(\displaystyle \angle(f_{k-1},f_k)\) szögek mindegyike kisebb \(\displaystyle 180^\circ\)-nál.
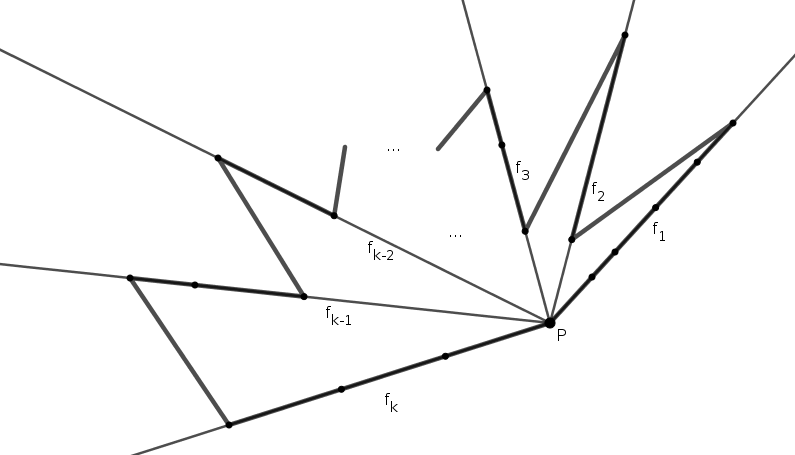
A pontokat ezután a következő algoritmus szerint köthetjük össze: elindulunk \(\displaystyle P\)-ből \(\displaystyle f_1\)-en és összekötjük az \(\displaystyle f_1\)-re illeszkedő pontokat. Az \(\displaystyle f_1\)-en lévő \(\displaystyle P\)-től legtávolabbi pontból \(\displaystyle f_2\) \(\displaystyle P\)-hez legközelebbi (\(\displaystyle P\)-től különböző) pontjára megyünk tovább az ábra szerint. Ezután \(\displaystyle P\)-től távolodva, \(\displaystyle f_2\)-n folytatjuk az összekötést, majd \(\displaystyle f_2\) \(\displaystyle P\)-től legtávolabbi pontjáról átmegyünk \(\displaystyle f_3\) \(\displaystyle P\)-hez legközelebbi pontjára. És így tovább, az ábra szerint. Az utolsó lépésben figyelnünk kell, \(\displaystyle f_{k-1}\) \(\displaystyle P\)-től legtávolabbi pontjáról az \(\displaystyle f_k\) \(\displaystyle P\)-től legtávolabbi pontjára lépünk tovább, majd azt \(\displaystyle f_k\)-n végighaladva bekötjük \(\displaystyle P\)-be, ezzel a töröttvonal bezáródik. A kapott töröttvonal nem metszi önmagát, az \(\displaystyle f_i\) – kezdőpontjuktól eltekintve diszjunkt – félegyeneseken nem alakulhat ki önátmetszés; összesen \(\displaystyle k-1\) darab további szakasz pedig \(\displaystyle k-1\) darab, egymástól diszjunkt, konvex, \(\displaystyle f_i\) félegyenest nem tartalmazó szögtartomány belsejében halad, ezeken szintén nem jöhet létre metszéspont. Ezzel az állítást beláttuk.
Statisztika:
62 dolgozat érkezett. 3 pontot kapott: Andó Viola, Arató Zita, Argay Zsolt, Csizmadia Miklós, Csonka Illés, Czett Mátyás, Fekete Richárd, Fey Dávid, Fülöp Csilla, Hervay Bence, Jánosik Máté, Kercsó-Molnár Anita, Laki Anna, Lovas Márton, Lőw László, Mácsai Dániel, Mezey Dorottya, Móra Márton Barnabás, Nádor Benedek, Nagy 551 Levente, Nagy Eszter Zsófia, Németh Márton, Páhán Anita Dalma, Reimann Kristóf, Szabó 991 Kornél, Szakács Ábel, Szűcs 064 Tamás, Terjék András József, Tóth 057 Bálint, Vakaris Klyvis, Varga Boldizsár, Világi Áron. 2 pontot kapott: 23 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2020. májusi matematika feladatai

