A B. 5103. feladat (2020. május)

B. 5103. Tegyük fel, hogy \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), \(\displaystyle x\), \(\displaystyle y\) és \(\displaystyle z\) olyan pozitív számok, amelyekre az \(\displaystyle a^2+b^2=c^2\) és az \(\displaystyle x^2+y^2=z^2\) egyenlőségek teljesülnek. Igazoljuk, hogy \(\displaystyle {(a+x)}^2+{(b+y)}^2\le {(c+z)}^2\), és határozzuk meg, hogy mikor áll fenn az egyenlőség.

Javasolta: Kiss Sándor (Nyíregyháza)

(3 pont)

A beküldési határidő 2020. június 10-én LEJÁRT.

Megoldás. Vegyünk egy \(\displaystyle (a+x)\cdot (b+y)\) méretű téglalapot és az oldalaival párhuzamosan osszuk fel \(\displaystyle a, x\), illetve \(\displaystyle b, y\) szeletekre az ábra szerint. Itt felhasználtuk, hogy \(\displaystyle a, b, x, y\) mind pozitív számok.

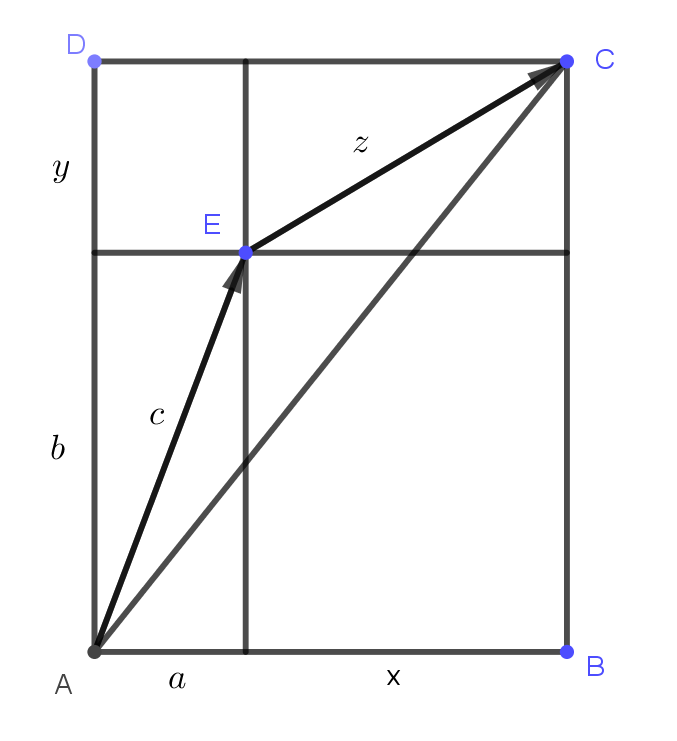
Az ábráról azonnal leolvasható, hogy az \(\displaystyle AE, EC, AC\) szakaszok rendre az \(\displaystyle a, b\), \(\displaystyle x, y\) és \(\displaystyle a+x, b+y\) befogójú derékszögű háromszög átfogói. Az \(\displaystyle E\) pont mindenképpen az \(\displaystyle ABCD\) téglalap belső pontja, tehát ebből a pontból az \(\displaystyle AC\) átfogó tompaszögben látszik. A háromszög-egyenlőtlenség alapján

\(\displaystyle c+z>AC.\)

Ezt négyzetre emelve

\(\displaystyle (c+z)^2>AC^2=(a+x)^2+(b+y)^2.\)

Egyenlőség akkor és csak akkor, ha az \(\displaystyle AEC\) háromszög elfajuló, az \(\displaystyle E\) pont az \(\displaystyle AC\) átlóra esik. Ekkor a két derékszögű háromszög hasonló, \(\displaystyle a:x=b:y\).

Megjegyzés. A feladat a Cauchy-Schwarz- féle egyenlőtlenség közvetlen következménye. Ugyanis legyen az \(\displaystyle (a,b)\) síkbeli vektor hossza \(\displaystyle c\), az \(\displaystyle (x, y)\) vektor hossza pedig \(\displaystyle z\). (Az \(\displaystyle a, b, x, y\) itt tetszőleges valós számok, míg \(\displaystyle c\) és \(\displaystyle z\) pozitív számok, hiszen egy-egy vektor hosszát jelentik.) Felírva a Cauchy-Schwarz- féle egyenlőtlenséget:

\(\displaystyle ax+by\le \sqrt{a^2+b^2}\sqrt{x^2+y^2}=cz.\)

Kettővel szorozva és a bal oldalhoz \(\displaystyle a^2+b^2+x^2+y^2\)-et, a jobb oldalhoz az ezzel megegyező \(\displaystyle c^2+z^2\)-et adva

\(\displaystyle a^2+2ax+x^2+b^2+2by+y^2\le c^2+2cz+z^2,\)

\(\displaystyle (a+x)^2+(b+y)^2\le (c+z)^2\)

éppen a bizonyítandó állítás adódik. Egyenlőség akkor és cak akkor, ha a két vektor párhuzamos és azonos irányítású, azaz amikor \(\displaystyle a:x=b:y\). Ebből a megoldásból láthatóan elegendő feltenni, hogy \(\displaystyle c\) és \(\displaystyle z\) pozitív számok, míg \(\displaystyle a,b,x,y\) tetszőleges valósak lehetnek.

Statisztika:

77 dolgozat érkezett.
3 pontot kapott:	Andó Viola, Arató Zita, Argay Zsolt, Baski Bence, Beke Csongor, Csizmadia Miklós, Czett Mátyás, Feczkó Nóra, Fekete Richárd, Fülöp Csilla, Füredi Erik Benjámin, Gábriel Tamás, Geretovszky Anna, Halász Henrik, Hervay Bence, Jánosik Máté, Kelemen Anna, Kercsó-Molnár Anita, Kerekes Boldizsár, Kovács Alex, Laki Anna, Metzger Ábris András, Mezey Dorottya, Mohay Lili Veronika, Móra Márton Barnabás, Nagy Eszter Zsófia, Páhán Anita Dalma, Reimann Kristóf, Richlik Bence, Sándor Péter, Seres-Szabó Márton, Somogyi Dalma, Szabó 248 Eszter, Szabó 991 Kornél, Szakács Ábel, Terjék András József, Tiderenczl Dániel, Tóth 057 Bálint, Vakaris Klyvis, Velich Nóra, Wiener Anna.
2 pontot kapott:	33 versenyző.
1 pontot kapott:	3 versenyző.

A KöMaL 2020. májusi matematika feladatai