 |
A B. 5104. feladat (2020. május) |
B. 5104. Legyenek az \(\displaystyle ABC\) háromszög beírt körének érintési pontjai az oldalakon \(\displaystyle A_1\), \(\displaystyle B_1\) és \(\displaystyle C_1\), a háromszög köréírt, illetve beírt körének sugara \(\displaystyle R\) és \(\displaystyle r\). Mutassuk meg, hogy az \(\displaystyle A_1B_1C_1\) és \(\displaystyle ABC\) háromszögek területének aránya \(\displaystyle r:2R\).
(4 pont)
A beküldési határidő 2020. június 10-én LEJÁRT.
Megoldás. Legyen a beírt kör középpontja \(\displaystyle O\), az \(\displaystyle A_1B_1C_1\) háromszög területe \(\displaystyle t\), az \(\displaystyle ABC\) háromszög területe pedig \(\displaystyle T\). Az \(\displaystyle A_1, B_1, C_1\) pontok érintési pontok, így az \(\displaystyle ABC\) háromszög beírt köre egyben az \(\displaystyle A_1B_1C_1\) háromszög körülírt köre is.
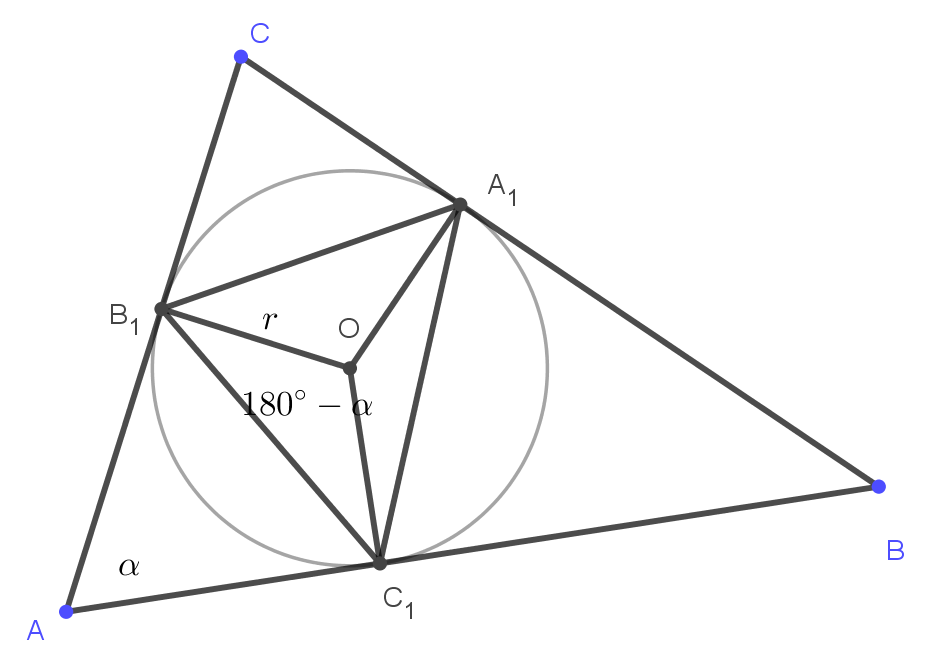
Az \(\displaystyle A_1B_1C_1\) háromszög csúcsait összekötjük a beírt kör \(\displaystyle O\) középpontjával. Ezzel felbontottuk ezt a háromszöget három egyenlő szárú háromszögre, melyeknek szárai mind \(\displaystyle r\) hosszúságúak. Az \(\displaystyle AB_1O\sphericalangle\) és az \(\displaystyle AC_1O\sphericalangle\) derékszögek, ezért az \(\displaystyle AB_1OC_1\) négyszögből \(\displaystyle B_1OC_1\sphericalangle=180^{\circ}-\alpha\). Hasonlóan látjuk, hogy \(\displaystyle C_1OA_1\sphericalangle=180^{\circ}-\beta\) és \(\displaystyle A_1OB_1\sphericalangle=180^{\circ}-\gamma\). Két oldal és a közbezárt szög segítségével felírjuk az egyenlő szárú háromszögek területét és felhasználjuk, hogy szög és kiegészítő szögének szinusza megegyezik.
\(\displaystyle t=\frac{1}{2}r^2\sin(180^{\circ}-\alpha)+\frac{1}{2}r^2\sin(180^{\circ}-\beta)+\frac{1}{2}r^2\sin(180^{\circ}-\gamma)=\frac{r^2}{2}(\sin\alpha+\sin\beta+\sin\gamma).\)
Az \(\displaystyle ABC\) háromszög területét a félkerülettel és a beírt kör sugarával határozzuk meg, majd felhasználjuk az általánosított szinusztételt, amely szerint
\(\displaystyle a=2R\sin\alpha, b=2R\sin\beta, c=2R\sin\gamma.\)
\(\displaystyle T=r\cdot s =\frac{r}{2}(a+b+c)=rR(\sin\alpha+\sin\beta+\sin\gamma).\)
Ezután már felírható a két terület aránya:
\(\displaystyle \frac{t}{T}=\frac{\frac{r^2}{2}(\sin\alpha+\sin\beta+\sin\gamma)}{rR(\sin\alpha+\sin\beta+\sin\gamma)}=\frac{r^2}{2Rr}=\frac{r}{2R}.\)
Statisztika:
48 dolgozat érkezett. 4 pontot kapott: Arató Zita, Balogh Ádám Péter, Bán-Szabó Áron, Baski Bence, Beinschroth Ninett, Beke Csongor, Biró 424 Ádám, Bognár 171 András Károly, Fekete Richárd, Fleiner Zsigmond, Füredi Erik Benjámin, Gábriel Tamás, Geretovszky Anna, Hervay Bence, Kercsó-Molnár Anita, Kerekes Boldizsár, Kovács 129 Tamás, Laki Anna, Lengyel Ádám, Lovas Márton, Mácsai Dániel, Nádor Benedek, Nagy 551 Levente, Németh Márton, Páhán Anita Dalma, Reimann Kristóf, Richlik Bence, Seres-Szabó Márton, Somogyi Dalma, Szabó 991 Kornél, Szakács Ábel, Sztranyák Gabriella, Szűcs 064 Tamás, Tiderenczl Dániel, Tóth 057 Bálint, Vakaris Klyvis, Velich Nóra, Wiener Anna, Zempléni Lilla. 3 pontot kapott: Halász Henrik, Mohay Lili Veronika, Molnár Lehel, Móricz Benjámin, Osztényi József. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 2 versenyző.
A KöMaL 2020. májusi matematika feladatai

