Problem B. 5104. (May 2020)

B. 5104. Let \(\displaystyle A_1\), \(\displaystyle B_1\) and \(\displaystyle C_1\) denote the points of tangency of the incircle of triangle \(\displaystyle ABC\) on the sides, and let \(\displaystyle R\) and \(\displaystyle r\) be the radii of the circumscribed and inscribed circles, respectively. Prove that the ratio of the areas of triangles \(\displaystyle A_1B_1C_1\) and \(\displaystyle ABC\) is \(\displaystyle r:2R\).

(4 pont)

Deadline expired on June 10, 2020.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen a beírt kör középpontja \(\displaystyle O\), az \(\displaystyle A_1B_1C_1\) háromszög területe \(\displaystyle t\), az \(\displaystyle ABC\) háromszög területe pedig \(\displaystyle T\). Az \(\displaystyle A_1, B_1, C_1\) pontok érintési pontok, így az \(\displaystyle ABC\) háromszög beírt köre egyben az \(\displaystyle A_1B_1C_1\) háromszög körülírt köre is.

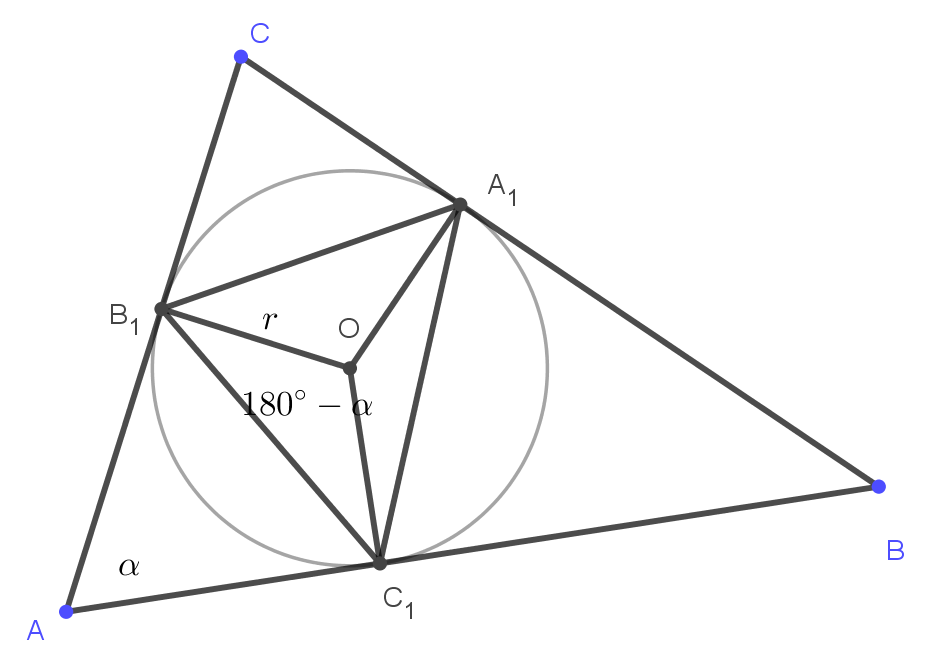
Az \(\displaystyle A_1B_1C_1\) háromszög csúcsait összekötjük a beírt kör \(\displaystyle O\) középpontjával. Ezzel felbontottuk ezt a háromszöget három egyenlő szárú háromszögre, melyeknek szárai mind \(\displaystyle r\) hosszúságúak. Az \(\displaystyle AB_1O\sphericalangle\) és az \(\displaystyle AC_1O\sphericalangle\) derékszögek, ezért az \(\displaystyle AB_1OC_1\) négyszögből \(\displaystyle B_1OC_1\sphericalangle=180^{\circ}-\alpha\). Hasonlóan látjuk, hogy \(\displaystyle C_1OA_1\sphericalangle=180^{\circ}-\beta\) és \(\displaystyle A_1OB_1\sphericalangle=180^{\circ}-\gamma\). Két oldal és a közbezárt szög segítségével felírjuk az egyenlő szárú háromszögek területét és felhasználjuk, hogy szög és kiegészítő szögének szinusza megegyezik.

\(\displaystyle t=\frac{1}{2}r^2\sin(180^{\circ}-\alpha)+\frac{1}{2}r^2\sin(180^{\circ}-\beta)+\frac{1}{2}r^2\sin(180^{\circ}-\gamma)=\frac{r^2}{2}(\sin\alpha+\sin\beta+\sin\gamma).\)

Az \(\displaystyle ABC\) háromszög területét a félkerülettel és a beírt kör sugarával határozzuk meg, majd felhasználjuk az általánosított szinusztételt, amely szerint

\(\displaystyle a=2R\sin\alpha, b=2R\sin\beta, c=2R\sin\gamma.\)

\(\displaystyle T=r\cdot s =\frac{r}{2}(a+b+c)=rR(\sin\alpha+\sin\beta+\sin\gamma).\)

Ezután már felírható a két terület aránya:

\(\displaystyle \frac{t}{T}=\frac{\frac{r^2}{2}(\sin\alpha+\sin\beta+\sin\gamma)}{rR(\sin\alpha+\sin\beta+\sin\gamma)}=\frac{r^2}{2Rr}=\frac{r}{2R}.\)

Statistics:

48 students sent a solution.
4 points:	Arató Zita, Balogh Ádám Péter, Bán-Szabó Áron, Baski Bence, Beinschroth Ninett, Beke Csongor, Biró 424 Ádám, Bognár 171 András Károly, Fekete Richárd, Fleiner Zsigmond, Füredi Erik Benjámin, Gábriel Tamás, Geretovszky Anna, Hervay Bence, Kercsó-Molnár Anita, Kerekes Boldizsár, Kovács 129 Tamás, Laki Anna, Lengyel Ádám, Lovas Márton, Mácsai Dániel, Nádor Benedek, Nagy 551 Levente, Németh Márton, Páhán Anita Dalma, Reimann Kristóf, Richlik Bence, Seres-Szabó Márton, Somogyi Dalma, Szabó 991 Kornél, Szakács Ábel, Sztranyák Gabriella, Szűcs 064 Tamás, Tiderenczl Dániel, Tóth 057 Bálint, Vakaris Klyvis, Velich Nóra, Wiener Anna, Zempléni Lilla.
3 points:	Halász Henrik, Mohay Lili Veronika, Molnár Lehel, Móricz Benjámin, Osztényi József.
2 points:	2 students.
1 point:	2 students.

Problems in Mathematics of KöMaL, May 2020