Problem B. 5108. (May 2020)

B. 5108. The points $\displaystyle A$, $\displaystyle B_1$, $\displaystyle B_2$, $\displaystyle B_3$, $\displaystyle C_1$, $\displaystyle C_2$, $\displaystyle C_3$, in this order, lie on the same line. On one side of this line, perpendicular rays $\displaystyle b_i$ are drawn from the points $\displaystyle B_i$, and semicircles $\displaystyle c_i$ are drawn with diameters $\displaystyle AC_i$ ($\displaystyle i=1,2,3$), as shown in the figure. Prove that if the region bounded by $\displaystyle b_1$, $\displaystyle c_1$, $\displaystyle b_2$, $\displaystyle c_2$ and the region bounded by $\displaystyle b_2$, $\displaystyle c_2$, $\displaystyle b_3$, $\displaystyle c_3$ both have inscribed circles then the region bounded by $\displaystyle b_1$, $\displaystyle c_1$, $\displaystyle b_3$, $\displaystyle c_3$ also has an inscribed circle.

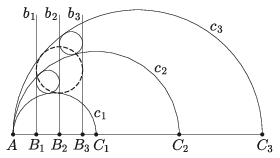
(5 pont)

Deadline expired on June 10, 2020.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen $\displaystyle i=1,2,3$-ra $\displaystyle d_i=\dfrac{AB_i}{2}$, és legyen $\displaystyle R_i$ a $\displaystyle c_i$ kör sugara. A feltételek szerint a $\displaystyle B_i$ pont az $\displaystyle AC_i$ szakasz belsejébe esik, vagyis $\displaystyle 2d_i=AB_i<AC_i=2R_i$, emiatt $\displaystyle R_i>d_i$.

Helyezzük el az ábrát a derékszögű koordináta-rendszerben úgy, hogy $\displaystyle A=(0,0)$, $\displaystyle B_i=(2d_i,0)$ és $\displaystyle C_i=(2R_i,0)$, a $\displaystyle c_i$ kör középpontja a $\displaystyle K_i=(R_i,0)$ pont. Vizsgáljuk meg, hogy a $\displaystyle b_1c_1b_2c_2$ tartományba milyen feltételek teljesülése esetén lehet beleírni a $\displaystyle P=(x,y)$ középpontú, $\displaystyle r$ sugarú $\displaystyle k$ kört.

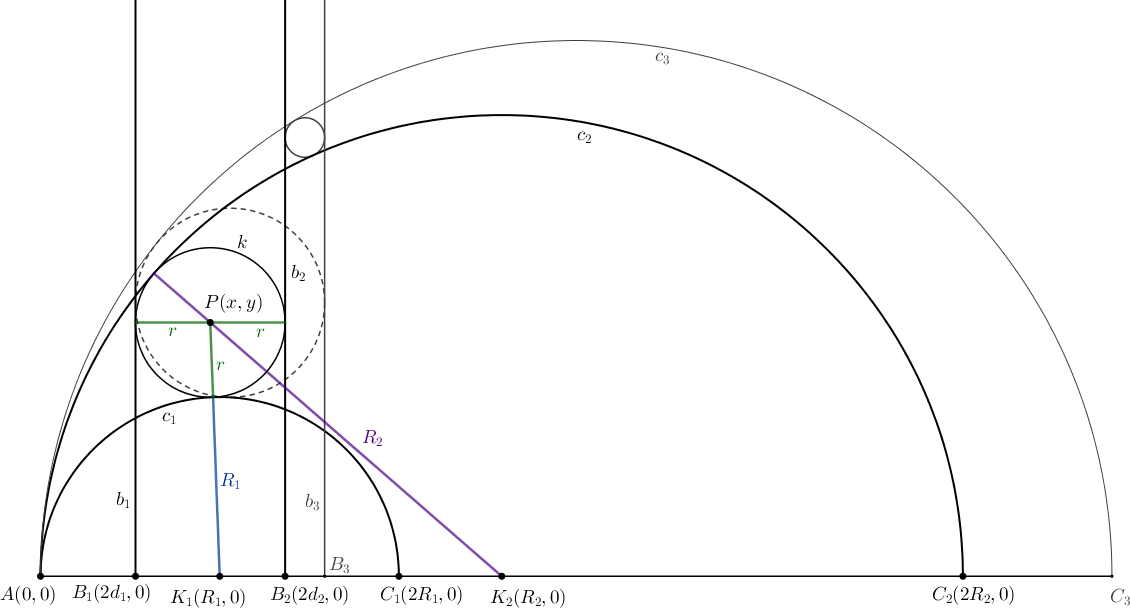
A $\displaystyle k$ akkor és csak akkor érinti az egymással párhuzamos $\displaystyle b_1$ és $\displaystyle b_2$ egyeneseket, ha a sugara a két egyenes távolságának fele, vagyis $\displaystyle r=\dfrac{B_1B_2}2=d_2-d_1$, a $\displaystyle k$ középpontja pedig a $\displaystyle b_1$ és $\displaystyle b_2$ egyenesek középvonalára esik, vagyis $\displaystyle x=\dfrac{OB_1+OB_2}2=d_2+d_1$. Az is szükséges, hogy $\displaystyle k$ a $\displaystyle c_2$ kör belsejében legyen, vagyis $\displaystyle r<R_2$; ez azért igaz, mert $\displaystyle r=d_2-d_1<d_2<R_2$.

Ezek után a harmadik ismeretlenre, $\displaystyle y$-ra két feltételünk maradt, a $\displaystyle k$-nak kívülről kell érintenie a $\displaystyle c_1$, és belülről kell érintenie a $\displaystyle c_2$ félkört is.

A $\displaystyle k$ akkor és csak akkor érinti kívülről a $\displaystyle c_1$ félkört, ha $\displaystyle y>0$ és $\displaystyle K_1P=R_1+r$. Négyzetre emelve,

$\displaystyle K_1P^2 = (x-R_1)^2+y^2 = (d_1+d_2-R_1)^2+y^2 \quad=\quad (R_1+r)^2 = (R_1+d_2-d_1)^2. $

Baloldalra rendezve $\displaystyle y^2$-et,

$$\begin{gather*} y^2 = (R_1+d_2-d_1)^2-(d_1+d_2-R_1)^2 = 4d_2(R_1-d_1). \tag{1} \end{gather*}$$

Hasonlóan, $\displaystyle k$ akkor és csak akkor érinti belülről a $\displaystyle c_2$ félkört, ha $\displaystyle r<R_2$ (ezt már ellenőriztük), $\displaystyle y>0$ és $\displaystyle K_2P=R_2-r$;

$$\begin{gather*} K_2P^2 = (x-R_2)^2+y^2 = (d_1+d_2-R_2)^2+y^2 \quad=\quad (R_2-r)^2 = (R_2-d_2+d_1)^2, \\ y^2 = (R_2-d_2+d_1)^2-(d_1+d_2-R_2)^2 = 4d_1(R_2-d_2). \end{gather*}$$

\tag2$\displaystyle $

Tehát a $\displaystyle k$ kör akkor és csak akkor létezik, ha az (1) és (2) egyenleteknek van egy közös, pozitív $\displaystyle y$ megoldása. Ehhez szükséges és elégséges, ha a jobboldalak egybeesnek és pozitívak, vagyis $\displaystyle 4d_2(R_1-d_1)=4d_1(R_2-d_2)>0$.

Vegyük azonban észre, hogy (1) és (2) jobb oldala is automatikusan pozitív, tehát csak azt kell ellenőriznünk, hogy $\displaystyle 4d_2(R_1-d_1)=4d_1(R_2-d_2)$ mikor teljesül. Átrendezve $\displaystyle d_2R_1=d_1R_2$, vagy $\displaystyle R_1R_2$-vel elosztva, $\displaystyle \dfrac{d_1}{R_1}=\dfrac{d_2}{R_2}$.

Az $\displaystyle 1,2$ helyett ugyanezt az $\displaystyle 1,3$ és $\displaystyle 2,3$ indexpárokra is elmondhatjuk, tehát a következőt kaptuk:

$$\begin{gather*} \text{A $\displaystyle b_ic_ib_jc_j$ tartományba akkor és csak akkor lehet kört írni, ha $\displaystyle \dfrac{d_i}{R_i}=\dfrac{d_j}{R_j}$.} \tag{*} \end{gather*}$$

A feltétel szerint a $\displaystyle b_1c_1b_2c_2$ és a $\displaystyle b_2c_2b_3c_3$ tartományokba is kört lehet írni, tehát $\displaystyle (*)$ szerint $\displaystyle \dfrac{d_1}{R_1}=\dfrac{d_2}{R_2}$ és $\displaystyle \dfrac{d_2}{R_2}=\dfrac{d_3}{R_3}$; akkor viszont $\displaystyle \dfrac{d_1}{R_1}=\dfrac{d_3}{R_3}$ is teljesül, tehát $\displaystyle (*)$ másik iránya szerint a $\displaystyle b_1c_1b_3c_3$ tartományba is kört lehet írni.

Megjegyzés. A feladat szorosan kapcsolódik a márciusi számban megjelent Térbe kilépő bizonyítások VI. c. cikkhez. Az ábrát $\displaystyle 90^\circ$-kal elforgatva és a Poincaré-féle félsíkmodellben értelmezve a $\displaystyle b_i$ és $\displaystyle b_j$, illetve $\displaystyle c_i$ és $\displaystyle c_j$ horociklusok távolsága is állandó.

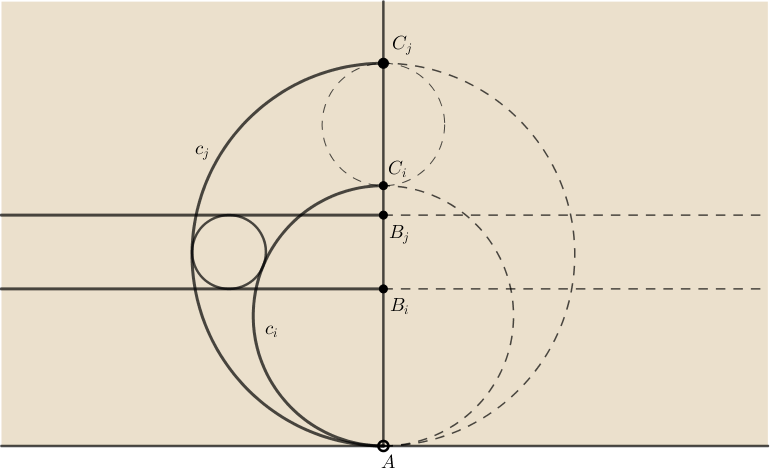
A négy horociklus közé írt kör akkor és csak akkor létezik, ha ez a két távolság megegyezik, azaz

$\displaystyle d(b_i,b_j) = d(B_i,B_j) = k\cdot\ln\dfrac{AB_j}{AB_i} = k\cdot\ln\dfrac{d_j}{d_i} \quad=\quad d(c_i,c_j) = d(C_i,C_j) = k\cdot\ln\dfrac{AC_j}{AC_i} = k\cdot\ln\dfrac{R_j}{R_i}, $

vagyis $\displaystyle \dfrac{d_j}{d_i} = \dfrac{R_j}{R_i}$, összhangban $\displaystyle (*)$-gal.

Statistics:

23 students sent a solution.

5 points: Argay Zsolt, Bán-Szabó Áron, Baski Bence, Beke Csongor, Czett Mátyás, Fekete Richárd, Fleiner Zsigmond, Füredi Erik Benjámin, Kerekes Boldizsár, Lengyel Ádám, Lovas Márton, Mácsai Dániel, Móra Márton Barnabás, Nádor Benedek, Németh Márton, Seres-Szabó Márton, Szabó 991 Kornél, Sztranyák Gabriella, Tiderenczl Dániel, Török Mátyás, Vakaris Klyvis, Varga Boldizsár, Velich Nóra.

Problems in Mathematics of KöMaL, May 2020

Already signed up?
New to KöMaL?