Problem B. 5124. (October 2020)

B. 5124. The base of a right pyramid is a square \(\displaystyle ABCD\), and the apex of the pyramid is \(\displaystyle E\). The skew edges \(\displaystyle AB\) and \(\displaystyle CE\) are connected by a transversal that is normal to both of them. The feet of the normal transversal are point \(\displaystyle P\) on the line segment \(\displaystyle AB\), and point \(\displaystyle Q\) on the line segment \(\displaystyle CE\). Given that \(\displaystyle Q\) bisects the edge \(\displaystyle CE\), determine the ratio \(\displaystyle AP: PB\), and calculate the angle enclosed between the lateral faces and the base of the pyramid.

(5 pont)

Deadline expired on November 10, 2020.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás.

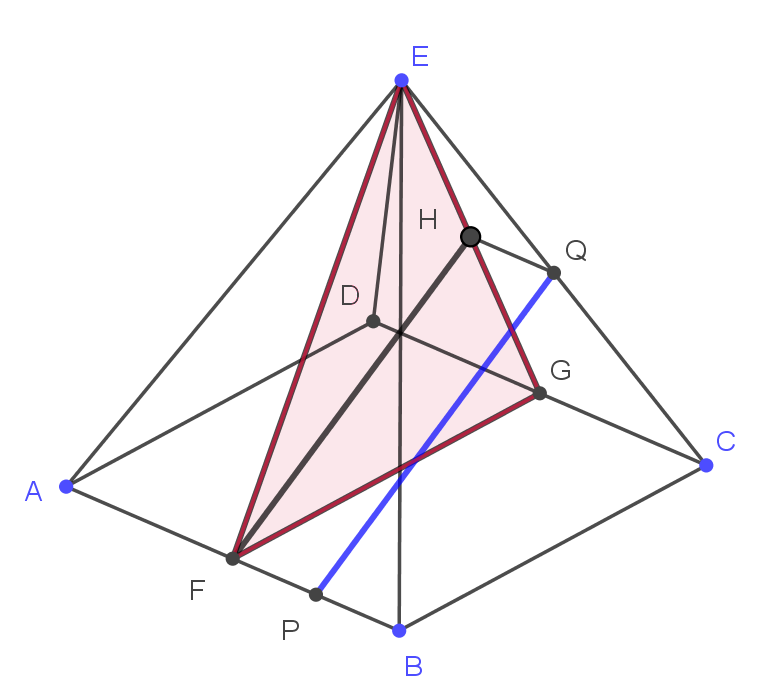
Legyen a gúla \(\displaystyle E\) csúcsából az \(\displaystyle AB\) élre bocsátott merőleges talppontja \(\displaystyle F\), a \(\displaystyle CD\) élre bocsátott merőleges talppontja \(\displaystyle G\), továbbá az \(\displaystyle EG\) oldalmagasságra az \(\displaystyle F\) pontból állított merőleges talppontja \(\displaystyle H\).

Az \(\displaystyle AB\) él párhuzamos a \(\displaystyle CD\) éllel, így a \(\displaystyle PQ\) normáltranszverzális merőleges a \(\displaystyle CD\)-re valamint \(\displaystyle EC\)-re, a \(\displaystyle CDE\) lap két nem párhuzamos egyenesére, tehát az egész lapsíkra is. A \(\displaystyle DC\) él merőleges az \(\displaystyle FGE\) síkra, hiszen \(\displaystyle DC\perp FG\) és \(\displaystyle DC\perp EG\). Így \(\displaystyle FH\), az \(\displaystyle EFG\) síkra illeszkedő egyenesként merőleges \(\displaystyle DC\)-re, valamint \(\displaystyle EG\)-re, így a \(\displaystyle CDE\) síkra is. Mivel ugyanarra a síkra merőlegesek, így \(\displaystyle PQ\) és \(\displaystyle FH\) párhuzamosak.

Az \(\displaystyle AB\) egyenes párhuzamos a \(\displaystyle CDE\) síkkal (hiszen annak \(\displaystyle CD\) egyenesével is párhuzamos), így minden pontja ugyanaolyan távol van a síktól, így \(\displaystyle FH=PQ\), és \(\displaystyle FPQH\) téglalap. Így \(\displaystyle HQ\parallel FP=AB \parallel GC\), és a párhuzamos szelők tétele miatt \(\displaystyle H\) felezi \(\displaystyle EG\) szakaszt. Az \(\displaystyle EFG\) háromszögben \(\displaystyle EF=EG\), hiszen a gúla szabályos. A fentiekben pedig már láttuk, hogy \(\displaystyle F\)-ből induló magasságvonala felezi a szemközti oldalt, tehát \(\displaystyle EF=FG\) is teljesül, az \(\displaystyle EFG\) háromszög szabályos. Az \(\displaystyle EF\) és \(\displaystyle FG\) is merőleges az \(\displaystyle AB\) élre, így \(\displaystyle EFG\sphericalangle=60^{\circ}\) az alaplap és oldallap hajlásszöge.

Az \(\displaystyle EGC\) háromszögben \(\displaystyle HQ\) középvonal, tehát \(\displaystyle HQ\) és a vele egyenlő hosszúságú \(\displaystyle FP\) az alapél negyede. Így azt is tudjuk, hogy a \(\displaystyle P\) pont \(\displaystyle 3:1\) arányban osztja ketté az \(\displaystyle AB\) szakaszt.

Statistics:

64 students sent a solution.
5 points:	Al-Hag Máté Amin, Andó Viola, Bán-Szabó Áron, Baski Bence, Beinschroth Ninett, Bencsik Ádám, Csizmadia Miklós, Csonka Illés, Diaconescu Tashi, Duchon Márton, Egyházi Hanna, Fekete Richárd, Győrffi Ádám György, Hegedűs Dániel, Hervay Bence, Kercsó-Molnár Anita, Kerekes Boldizsár, Koleszár Domonkos, Kovács 129 Tamás, Kökényesi Márk Péter, Lengyel Ádám, Lovas Márton, Lőw László, Mácsai Dániel, Márton Kristóf, Mátéfy Ádám , Móra Márton Barnabás, Nádor Benedek, Nagy 551 Levente, Németh Márton, Nguyen Bich Diep, Nyárfádi Patrik, Osztényi József, Rareș Polenciuc, Révész Máté, Richlik Bence, Romaniuc Albert-Iulian, Seláf Bence, Seres-Szabó Márton, Simon László Bence, Somogyi Dalma, Szakács Ábel, Szeibert Barnabás, Terjék András József, Török Ágoston, Trombitás Karolina Sarolta, Varga Boldizsár, Velich Nóra, Virág Rudolf.
4 points:	9 students.
3 points:	4 students.
1 point:	1 student.
0 point:	1 student.

Problems in Mathematics of KöMaL, October 2020