Problem B. 5133. (November 2020)

B. 5133. Given six points in the space, no four of which are coplanar, prove that they can be divided into two sets of three such that the two triangular plates spanned by the two sets of three points should intersect each other.

(6 pont)

Deadline expired on December 10, 2020.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Ha néhány térbeli pont közül semelyik négy nem esik egy síkra, azt mondjuk röviden, hogy a pontok általános helyzetűek. Továbbá néhány térbeli pont konvex pozícióban van, ha nincs köztük olyan, amit tartalmaz a többi pont konvex burka.

A bizonyítást két segédállításra bontjuk.

1. segédállítás. Öt általános helyzetű, konvex pozícióban lévő térbeli pontból kiszínezhető kettő kékre és a maradék három pirosra úgy, hogy a kék pontokat összekötő szakasz és a piros csúcsok által meghatározott háromszöglap metszi egymást.

Az 1. segédállítás bizonyítása. Tekintsük az adott öt pont közül valamely négyet, mondjuk az \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) és \(\displaystyle D\) pontokat. Ezek egy tetraédert határoznak meg, ezen tetraéder lapsíkjai a teret \(\displaystyle 15\) összefüggő tartományra bontják. A keletkező tartományok közül egy a tetraéder belseje. Négy tartomány a határán tartalmazza a tetraéder valamely lapját, ezeket lap fölötti tartományoknak nevezzük. További hat tartomány a határán tartalmazza a tetraéder valamely élét (de lapját nem), ezeket él fölötti tartományoknak nevezzük. Végül négy tartomány a határán tartalmazza a tetraéder valamely csúcsát (de élét nem), ezeket csúcs fölöttti tartományoknak nevezzük.

Vizsgáljuk az eseteket aszerint, hogy az ötödik, az \(\displaystyle E\) pont milyen tartományba esik.

Az \(\displaystyle E\) pont nem eshet az \(\displaystyle ABCD\) tetraéder belsejébe, mert a pontok a feltevés szerint konvex pozícióban vannak. Szintén nem eshet csúcs fölötti tartományba, hiszen ha pl. az \(\displaystyle A\) csúcs fölötti tartományban lenne, akkor a \(\displaystyle BCDE\) tetraéder belesejében tartalmazná az \(\displaystyle A\) pontot.

Ha az \(\displaystyle E\) pont egy lap, pl. \(\displaystyle ABC\) fölötti tartományba esik, akkor a \(\displaystyle DE\) szakasz metszi az \(\displaystyle ABC\) háromszöget. Végül, ha az \(\displaystyle E\) pont egy él, pl. \(\displaystyle AB\) fölötti tartományba esik, akkor az \(\displaystyle AB\) szakasz metszi a \(\displaystyle CDE\) háromszöget. (Lásd az ábrán a két esetet.)

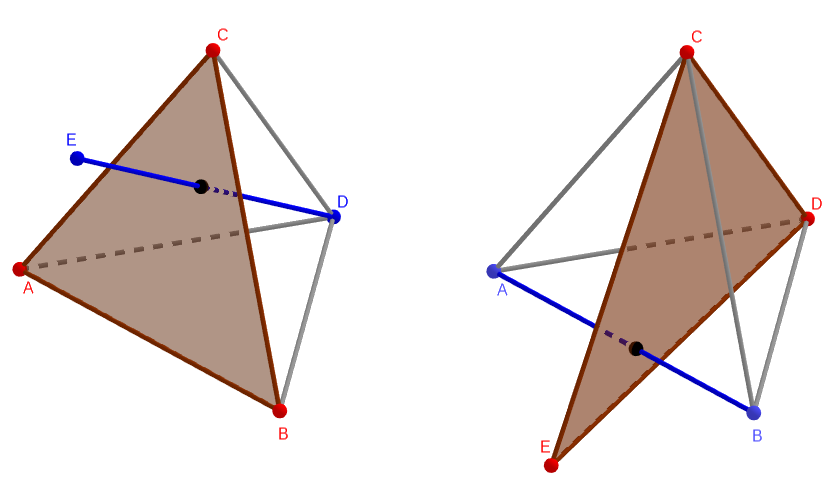
Ezzel az 1. segédállítást beláttuk.

2. segédállítás. Hat általános helyzetű térbeli pont között található öt, ami konvex pozícióban van.

Az 2. segédállítás bizonyítása. Tekintsük a pontok konvex burkát. Ha ennek a poliédernek legalább öt csúcsa van, akkor a csúcsok konvex pozícióban vannak, és az állítás teljesül. Feltehetjük tehát, hogy a pontok konvex burka az \(\displaystyle ABCD\) tetraéder, aminek a belsejében vannak az \(\displaystyle E\) és \(\displaystyle F\) pontok.

Mivel az \(\displaystyle ABCE\), \(\displaystyle ABDE\), \(\displaystyle ACDE\) és \(\displaystyle BCDE\) tetraéderek együttesen lefedik az \(\displaystyle ABCD\) tetraédert, így valamelyik, mondjuk \(\displaystyle ABCE\) tartalmazza \(\displaystyle F\)-t. Mivel \(\displaystyle ABCE\) nem tartalmazza \(\displaystyle D\)-t, így az \(\displaystyle FD\) szakasz valamely lapján elmetszi \(\displaystyle ABCE\) felszínét, feltehetjük, hogy ez a lap \(\displaystyle ABE\). (Mivel \(\displaystyle F\) és \(\displaystyle D\) az \(\displaystyle ABC\) sík ugyanazon partján vannak, így az \(\displaystyle ABC\) lapot nem metszheti, a maradék három lap szerepe szimmetrikus.) Ekkor könnyen ellenőrizhető, hogy \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle D\), \(\displaystyle E\) és \(\displaystyle F\) konvex pozícióban vannak.

Ezzel az 2. segédállítást is beláttuk.

Végül a feladat állítását a segédállítások segítségével a következőképpen igazolhatjuk: a 2. segédállítás szerint válasszunk ki öt pontot, amelyek konvex pozícióban vannak. Színezzük ki ezeket a pontokat az 1. segédállítás szerint, továbbá a hatodik, kimaradó pont is legyen kék. Ekkor a kék és a piros háromszög nyilvánvalóan metszi egymást. Ezzel a bizonyítást befejeztük.

Megjegyzés: Az 1. segédállítás a három dimenziós Radon-tétel generikus esete. A 2. segédállítás pedig a híres, magyar vonatkozású, és a KöMaLhoz is erősen kötődő Happy end-probléma három dimenziós (szintén jól ismert) változata.

Statistics:

34 students sent a solution.
6 points:	Bán-Szabó Áron, Duchon Márton, Fey Dávid, Kercsó-Molnár Anita, Kovács 129 Tamás, Kökényesi Márk Péter, Lőw László, Molnár-Szabó Vilmos, Nádor Benedek, Seres-Szabó Márton, Simon László Bence, Terjék András József, Varga Boldizsár, Virág Rudolf.
5 points:	Bognár 171 András Károly, Csizmadia Miklós, Kalocsai Zoltán, Lovas Márton, Nagy 551 Levente.
4 points:	3 students.
3 points:	5 students.
2 points:	2 students.
1 point:	1 student.
0 point:	4 students.

Problems in Mathematics of KöMaL, November 2020