Problem B. 5135. (December 2020)

B. 5135. The feet of the altitudes drawn from vertices \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) of an acute-angled triangle \(\displaystyle ABC\) are \(\displaystyle A_1\), \(\displaystyle B_1\) and \(\displaystyle C_1\), respectively; and the midpoints of the altitudes \(\displaystyle AA_1\) and \(\displaystyle BB_1\) are \(\displaystyle G\) and \(\displaystyle H\), respectively. Prove that the circumscribed circle of triangle \(\displaystyle C_1GH\) passes through the midpoint \(\displaystyle F\) of side \(\displaystyle AB\).

Proposed by B. Bíró, Eger

(4 pont)

Deadline expired on January 11, 2021.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Használjuk az ábra jelöléseit, legyen \(\displaystyle M\) az \(\displaystyle ABC\) háromszög magasságpontja. Megmutatjuk, hogy az \(\displaystyle MF\) szakasz a \(\displaystyle C_1\), \(\displaystyle G\) és \(\displaystyle H\) pontok mindegyikéből derékszög alatt látszik, ebből az állítás a Thalész-tétel megfordítása segítségével azonnal következik.

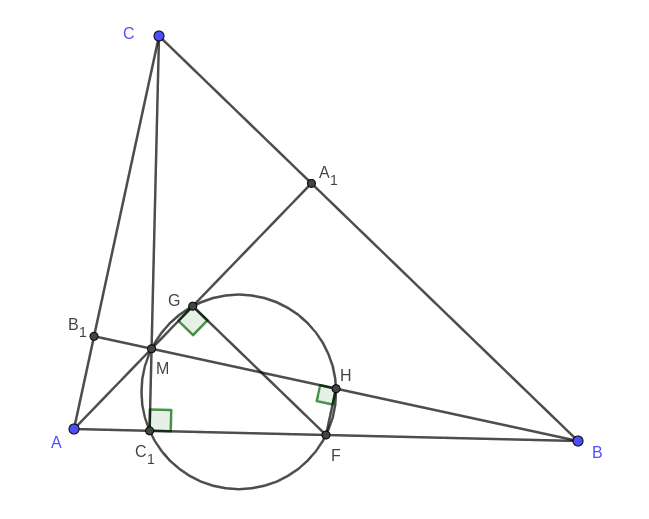
Mivel \(\displaystyle M\) illeszkedik a \(\displaystyle CC_1\) szakaszra, és \(\displaystyle CC_1\perp AB\), így \(\displaystyle MC_1F\angle\) valóban derékszög.

Az \(\displaystyle ABA_1\) háromszögben \(\displaystyle FG\) a \(\displaystyle BA_1\) befogóval párhuzamos középvonal, így \(\displaystyle FG\perp AA_1\), tehát \(\displaystyle FGM\angle\) derékszög. Hasonlóan, az \(\displaystyle ABB_1\) háromszögben \(\displaystyle FH\) az \(\displaystyle AB_1\) befogóval párhuzamos középvonal, ami miatt \(\displaystyle FH\perp BB_1\), s így \(\displaystyle FHM\angle\) is derékszög. Ezzel az állítást beláttuk.

Diszkusszió: a \(\displaystyle C_1GH\) kör jól definiált, nyilvánvalóan \(\displaystyle C_1\neq G\) és \(\displaystyle C_1\neq H\); míg \(\displaystyle G=H\) esetén az \(\displaystyle ABA_1B_1\) négyszög átlói felezve metszenék egymást, azaz a négyszög paralelogramma lenne, s az \(\displaystyle ABC\) háromszögnek lenne két párhuzamos oldala. A \(\displaystyle C_1,G,H\) pontok tehát páronként különböznek. Továbbá \(\displaystyle FG\parallel BA_1=BC\) és \(\displaystyle FH\parallel AB_1=AC\) miatt a három pont nem eshet egy egyenesre.

A \(\displaystyle C_1=F\), \(\displaystyle G=M\) és \(\displaystyle H=M\) esetekben a bizonyításban használt szögek esetleg nem jönnek létre, de a \(\displaystyle C_1\), \(\displaystyle G\) és \(\displaystyle H\) pontok ilyenkor is nyilvánvalóan illeszkednek az \(\displaystyle MF\) szakasz Thalész-körére.

Statistics:

93 students sent a solution.
4 points:	Győrffi Ádám György, Horváth 530 Mihály, Kercsó-Molnár Anita, Nagy 551 Levente, Romaniuc Albert-Iulian, Szanyi Attila, Török Ágoston, Zömbik Barnabás.
3 points:	64 students.
2 points:	16 students.
1 point:	4 students.
0 point:	1 student.

Problems in Mathematics of KöMaL, December 2020