 Problem B. 5139. (December 2020)
Problem B. 5139. (December 2020)
B. 5139. The diagonals of a convex quadrilateral \(\displaystyle ABCD\) intersect at \(\displaystyle M\). The area of triangle \(\displaystyle ADM\) is greater than that of triangle \(\displaystyle BCM\). The midpoint of side \(\displaystyle BC\) of the quadrilateral is \(\displaystyle P\), and the midpoint of side \(\displaystyle AD\) is \(\displaystyle Q\), \(\displaystyle AP+AQ=\sqrt2\,\). Prove that the area of quadrilateral \(\displaystyle ABCD\) is smaller than 1.
(5 pont)
Deadline expired on January 11, 2021.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Az \(\displaystyle ABCD\) négyszög területét az \(\displaystyle APQ\) háromszög területével fogjuk összehasonlítani. A különböző három- és négyszögek területét \(\displaystyle [...]\) fogja jelölni.
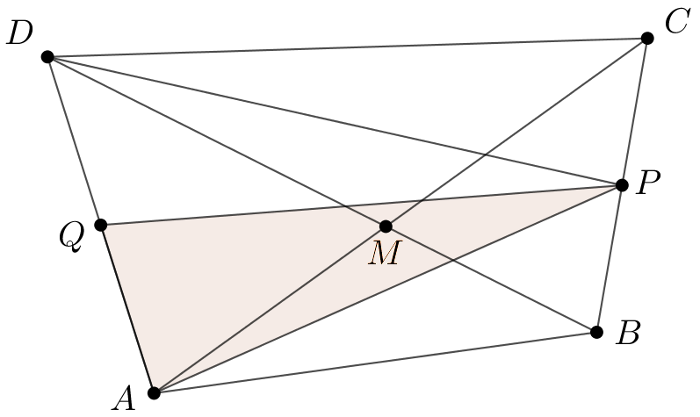
A feltétel szerint \(\displaystyle [ADM]>[BCM]\), ezért
| \(\displaystyle [ABCD] = [ABD]+[BCM]+[CDM] < [ABD]+[ADM]+[CDM] = [ABD]+[ACD]. \) | \(\displaystyle (1) \) |
Az \(\displaystyle ABD\), \(\displaystyle ACD\) és \(\displaystyle APD\) háromszögek \(\displaystyle AD\) oldala közös. Mivel \(\displaystyle P\) a \(\displaystyle BC\) szakasz felezőpontja, a \(\displaystyle P\) pont távolsága az \(\displaystyle AD\) egyenestől megyegyezik a \(\displaystyle B\) és a \(\displaystyle C\) pontoknak az \(\displaystyle AD\) egyenestől mért távolságainak átlagával, ezért
| \(\displaystyle [ABD]+[ACD] = 2[APD]. \) | \(\displaystyle (2) \) |
Az \(\displaystyle APQ\) és az \(\displaystyle APD\) háromszögeknek a \(\displaystyle P\)-ből induló magassága közös, a \(\displaystyle P\)-vel szemközti oldalaik aránya \(\displaystyle AQ:AD=1:2\); ebből láthatjuk, hogy
| \(\displaystyle [APD] = 2[APQ]. \) | \(\displaystyle (3) \) |
Az \(\displaystyle APQ\) háromszög területét megbecsüljük az \(\displaystyle AP\) és \(\displaystyle AQ\) oldalak szorzatával, majd alkalmazzuk a számtani és mértani közepek közötti egyenlőtlenséget az \(\displaystyle AP\) és \(\displaystyle AQ\) távolságokra:
| \(\displaystyle [APQ] \le \frac12\cdot AP\cdot AQ \le \frac12\left(\frac{AP+AQ}{2}\right)^2 = \frac12\left(\frac{\sqrt{2}}{2}\right)^2 = \frac14. \) | \(\displaystyle (4) \) |
Az (1–4) összefüggéseket kombinálva:
\(\displaystyle [ABCD] < [ABD]+[ACD] = 2[APD] = 4[APQ] \le 4\cdot\frac14 = 1. \)
Ezzel igazoltuk, hogy \(\displaystyle [ABCD]<1\).
Statistics:
44 students sent a solution. 5 points: Balogh Ádám Péter, Bán-Szabó Áron, Baski Bence, Bencsik Ádám, Bognár 171 András Károly, Csilling Dániel, Csonka Illés, Diaconescu Tashi, Duchon Márton, Feczkó Nóra, Fekete Richárd, Hajdú Bálint, Hegedűs Dániel, Kalocsai Zoltán, Kercsó-Molnár Anita, Koleszár Domonkos, Kovács 129 Tamás, Lengyel Ádám, Lovas Márton, Mácsai Dániel, Márton Kristóf, Mohay Lili Veronika, Molnár-Szabó Vilmos, Nádor Benedek, Nagy 429 Leila, Nagy 551 Levente, Németh Márton, Osztényi József, Páhán Anita Dalma, Seres-Szabó Márton, Somogyi Dalma, Sztranyák Gabriella, Terjék András József, Török Ágoston, Trombitás Karolina Sarolta, Varga Boldizsár. 4 points: Andó Viola, Győrffi Ádám György, Rareș Polenciuc, Sógor Bence, Velich Nóra. 3 points: 2 students. 1 point: 1 student.
Problems in Mathematics of KöMaL, December 2020
