 Problem B. 5152. (February 2021)
Problem B. 5152. (February 2021)
B. 5152. Determine those positive integers greater than \(\displaystyle 1\) whose positive divisors can all be written on the circumference of a circle so that the ratio of every adjacent pair should be a prime.
Proposed by D. Lenger, Budapest and G. Szűcs, Szikszó
(5 pont)
Deadline expired on March 10, 2021.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Először vizsgáljuk azt az esetet, amikor a számnak egyféle prímosztója van, vagyis prímhatvány. Ha \(\displaystyle n=p^\alpha\), akkor az 1 szomszédja csak \(\displaystyle p\) lehet, vagyis \(\displaystyle \alpha\geq 2\) esetén nem létezik megfelelő felírás, hiszen ilyenkor az 1-nek két különböző szomszédja is van. Ha \(\displaystyle \alpha=1\), akkor az egyetlen lehetséges sorrend (\(\displaystyle 1\) és \(\displaystyle p\) a két szám a körvonalon) megfelelő. A prímhatványok közül tehát pontosan a prímek azok, melyekre van megfelelő felírás.
A továbbiakban azokat az eseteket vizsgáljuk, amikor az \(\displaystyle n\) számnak legalább két különböző prímosztója is van. Legyen a szám prímtényezős felbontása \(\displaystyle n=p_1^{\alpha_1}p_2^{\alpha_2}\dots p_r^{\alpha_r}\) (ahol \(\displaystyle r\geq2\)). Ha \(\displaystyle d\) az \(\displaystyle n\) szám egy pozitív osztója, akkor \(\displaystyle d=p_1^{\beta_1}p_2^{\beta_2}\dots p_r^{\beta_r}\) valamely \(\displaystyle 0\leq \beta_1 \leq \alpha_1, \dots, 0\leq \beta_r\leq \alpha_r\) kitevőkkel. Ebből következik az a jól ismert összefüggés is, hogy \(\displaystyle n\) pozitív osztóinak száma \(\displaystyle (\alpha_1+1)(\alpha_2+1)\dots(\alpha_r+1)\).
Jelölje \(\displaystyle \Omega(d)=\beta_1+\beta_2+\dots+\beta_r\) a \(\displaystyle d\) szám multiplicitással számolt prímosztóinak számát. Ha van megfelelő felírás, akkor a körvonalra írt számokon lépegetve minden lépésben 1-gyel változik a prímosztók \(\displaystyle \Omega\) száma. Így \(\displaystyle \Omega(d)\) felváltva lesz páros, illetve páratlan, egy teljes kört megtéve viszont ugyanahhoz a számhoz érünk vissza, így az osztók számának párosnak kell lennie. Tehát megfelelő felírás csak akkor lehet, ha az osztók \(\displaystyle (\alpha_1+1)(\alpha_2+1)\dots(\alpha_r+1)\) száma páros, vagyis ha legalább az egyik \(\displaystyle \alpha_i\) kitevő páratlan (azaz a szám nem négyzetszám).
Vizsgáljuk meg külön az \(\displaystyle r=2\) esetet. Legyen tehát \(\displaystyle n=p_1^{\alpha_1}p_2^{\alpha_2}\), és mondjuk \(\displaystyle \alpha_1\) páratlan. A következő sorrend megfelelő:
$$\begin{multline*} 1,p_1,p_1^2,\dots,p_1^{\alpha_1}, p_1^{\alpha_1}p_2, \dots, p_1^{\alpha_1}p_2^{\alpha_2},p_1^{\alpha_1-1}p_2^{\alpha_2},p_1^{\alpha_1-1}p_2^{\alpha_2-1},\dots,p_1^{\alpha_1-1}p_2,p_1^{\alpha_1-2}p_2,p_1^{\alpha_1-2}p_2^2,\dots,p_1^{\alpha_1-2}p_2^{\alpha_2},\\ p_1^{\alpha_1-3}p_2^{\alpha_2},\dots,p_1^{\alpha_1-3}p_2,\dots,p_1p_2,\dots,p_1p_2^{\alpha_2},p_2^{\alpha_2}, \dots, p_2. \end{multline*}$$Példaként \(\displaystyle \alpha_1=5,\alpha_2=4\) esetén a következőképpen néz ki a sorrend (a vastagított vonal mutatja, hogy milyen sorrendben kerülnek a körvonalra az osztók):
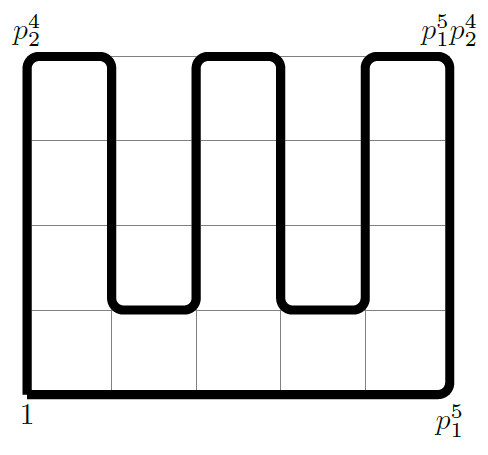
Ezzel beláttuk, hogy ha \(\displaystyle r=2\), akkor páros sok osztó esetén van megfelelő felírás (páratlan sok osztó esetén pedig nincsen).
Most belátjuk \(\displaystyle r\)-re vonatkozó teljes indukcióval, hogy ez \(\displaystyle r>2\) esetén is így van. Tegyük fel tehát, hogy az \(\displaystyle n\) számnak \(\displaystyle r>2\) különböző prímtényezője van, és legalább egyikük kitevője páratlan \(\displaystyle n\) prímtényezős felbontásában. Legyen az egyik prímhatvány \(\displaystyle n\) prímtényezős felbontásában \(\displaystyle q^\beta\), ahol \(\displaystyle q\)-t úgy választjuk meg, hogy a többi prímtényező közül legalább egyik kitevője páratlan legyen. (Például ha van páros kitevővel szerepelő prím, akkor azt választjuk \(\displaystyle q\)-nak, ha nincs, akkor pedig \(\displaystyle q\) bármelyik prímosztó lehet.) Tehát \(\displaystyle n=q^\beta n'\), ahol \(\displaystyle n'\)-nek \(\displaystyle r-1\) féle prímosztója van, és legalább egyik páratlan kitevővel szerepel \(\displaystyle n'\) prímtényezős felbontásában. Ezek alapján \(\displaystyle n'\)-nek páros sok osztója van, melyek felírhatók megfelelő módon a körvonalra, mondjuk \(\displaystyle d_1,d_2,\dots,d_{2t}\) sorrendben. Tehát itt két szomszédos \(\displaystyle d_i\) hányadosa (beleértve a \(\displaystyle d_{2t}\) és \(\displaystyle d_1\) párt is) mindig prímszám.
Az \(\displaystyle n\) szám (pozitív) osztói a \(\displaystyle d_iq^j\) alakú számok, ahol \(\displaystyle 1\leq i\leq 2t\) és \(\displaystyle 0\leq j\leq \beta\). Ezek egy megfelelő sorrendje a következő:
$$\begin{multline*} d_1,d_1q,\dots d_1q^{\beta},d_2q^{\beta},d_2q^{\beta-1},\dots,d_2, d_3, d_3q,\dots ,d_3q^\beta,d_4q^\beta,\dots,d_4,\dots,\\ d_{2t-2},d_{2t-1},d_{2t-1}q,\dots,d_{2t-1}q^\beta,d_{2t}q^\beta,\dots,d_{2t}q,d_{2t}. \end{multline*}$$Ezzel beláttuk, hogy \(\displaystyle n\) osztóinak is van megfelelő felírása.
Összefoglalva tehát, pontosan a következő esetekben van megfelelő felírás:
- ha \(\displaystyle n\)-nek legalább két prímosztója van, melyek közül legalább az egyiknek páratlan a kitevője \(\displaystyle n\) prímtényezős felbontásában (tehát \(\displaystyle n\) nem négyzetszám),
- vagy ha \(\displaystyle n\) prím.
Statistics:
58 students sent a solution. 5 points: Bán-Szabó Áron, Baski Bence, Bencsik Ádám, Csizmadia Miklós, Duchon Márton, Farkas 512 Izabella, Fekete Richárd, Fülöp Csilla, Hegedűs Dániel, Kalocsai Zoltán, Kercsó-Molnár Anita, Kerekes Boldizsár, Kovács 129 Tamás, Kökényesi Márk Péter, Lovas Márton, Mácsai Dániel, Molnár-Szabó Vilmos, Móra Márton Barnabás, Móricz Benjámin, Nádor Benedek, Nagy 551 Levente, Németh Márton, Páhán Anita Dalma, Sándor Péter, Seres-Szabó Márton, Somogyi Dalma, Szanyi Attila, Sztranyák Gabriella, Török Ágoston, Trombitás Karolina Sarolta, Varga Boldizsár, Wiener Anna. 4 points: Ben Gillott, Dezső Kende Barnabás, Nagy 429 Leila, Simon László Bence, Zömbik Barnabás. 3 points: 3 students. 2 points: 5 students. 1 point: 4 students. 0 point: 8 students. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, February 2021
