Problem B. 5155. (February 2021)

B. 5155. The convex quadrilateral \(\displaystyle ABCD\) has no parallel sides, and the intersection of lines \(\displaystyle AB\) and \(\displaystyle CD\) is \(\displaystyle M\). Point \(\displaystyle X\) is moving along the interior of side \(\displaystyle AB\), and point \(\displaystyle Y\) is moving along the interior of side \(\displaystyle CD\) so that the equality \(\displaystyle AX:XB=DY:YC\) remains true. Show that the circles \(\displaystyle MXY\) all have another common point, different from \(\displaystyle M\).

(5 pont)

Deadline expired on March 10, 2021.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Az \(\displaystyle A\) és \(\displaystyle B\), továbbá \(\displaystyle C\) és \(\displaystyle D\) pontok felcserélésével az állítás önmagába megy át, ezért elég az állítást abban az esetben igazolnunk, amikor az \(\displaystyle M\) pont a \(\displaystyle BA\) és \(\displaystyle CD\) félegyeneseken van. Legyen \(\displaystyle \alpha=BMC\sphericalangle\).

Tekintsük azt a \(\displaystyle \varphi\) forgatva nyújtást, amely az \(\displaystyle A\) pontot \(\displaystyle D\)-be, a \(\displaystyle B\) pontot pedig a \(\displaystyle C\) pontba viszi, tehát \(\displaystyle \varphi(A)=D\) és \(\displaystyle \varphi(B)=C\). A \(\displaystyle \varphi\) középpontját jelöljük \(\displaystyle Q\)-val; azt fogjuk megmutatni, hogy az \(\displaystyle MXY\) köröknek \(\displaystyle Q\) a közös pontja.

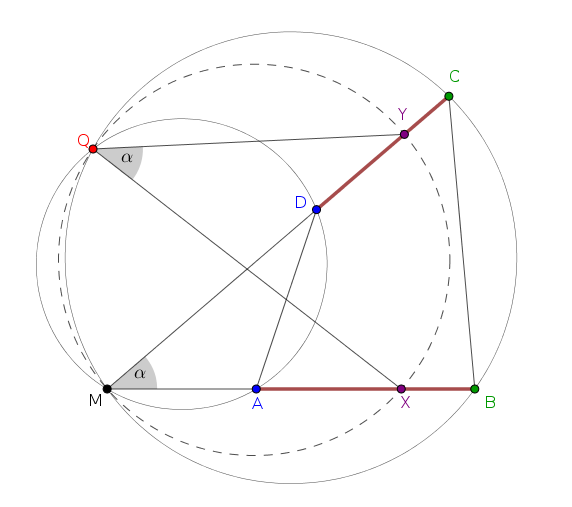
Meg kell jegyeznünk, hogy a forgatva nyújtás középpontja nem lehet az \(\displaystyle M\) pont: ha a középpont az \(\displaystyle M\) lenne, akkor \(\displaystyle MA:MB=MD:MC\) lenne, akkor viszont a párhuzamos szelők tételének megfordítása miatt az \(\displaystyle AD\) és \(\displaystyle BC\) egyenesek párhuzamosak lennének, márpedig a feladat kikötötte, hogy az \(\displaystyle ABCD\) négyszögnek nincsenek párhuzamos oldalai. Ezért \(\displaystyle M\) és \(\displaystyle Q\) két különböző pont.

Az \(\displaystyle X\) és az \(\displaystyle Y\) pont azonos arányban osztja az \(\displaystyle AB\) és \(\displaystyle DC\) szakaszokat, ezért ezek egymás képei: \(\displaystyle \varphi(X)=Y\). A forgatva nyújtásnak az (irányított) szöge az \(\displaystyle AB\) és \(\displaystyle CD\) szakaszok szöge, vagyis \(\displaystyle \alpha\); ezért \(\displaystyle XQY\sphericalangle = \alpha = BMC\sphericalangle = XMY\sphericalangle\). Ezeknek a szögeknek az irányítása is megegyezik, ezért az \(\displaystyle X,Y,M,Q\) pontok valóban egy körön vannak.

Megjegyzés. Az \(\displaystyle MXY\) körök két fontos határesete (az \(\displaystyle X=A\), \(\displaystyle Y=D\), illetve az \(\displaystyle X=B\), \(\displaystyle Y=C\) esetekben) az \(\displaystyle MAD\) és az \(\displaystyle MBC\) kör. Ezért a \(\displaystyle Q\) pont az \(\displaystyle MAD\) és \(\displaystyle MBC\) körök második, \(\displaystyle M\)-től különböző metszéspontja.

Statistics:

39 students sent a solution.
5 points:	Bán-Szabó Áron, Baski Bence, Csizmadia Miklós, Diaconescu Tashi, Duchon Márton, Fekete Richárd, Hegedűs Dániel, Kalocsai Zoltán, Kercsó-Molnár Anita, Koleszár Domonkos, Kökényesi Márk Péter, Metzger Ábris András, Mohay Lili Veronika, Nagy 551 Levente, Páhán Anita Dalma, Simon László Bence, Terjék András József, Varga Boldizsár.
4 points:	Beinschroth Ninett, Ben Gillott, Bencsik Ádám, Bencsik Dávid, Kovács 129 Tamás, Mácsai Dániel, Molnár-Szabó Vilmos, Móra Márton Barnabás, Nádor Benedek, Németh Márton, Rareș Polenciuc, Sándor Péter, Seres-Szabó Márton, Somogyi Dalma, Sztranyák Gabriella, Velich Nóra, Virág Rudolf.
3 points:	2 students.
2 points:	1 student.
1 point:	1 student.

Problems in Mathematics of KöMaL, February 2021