Problem B. 5163. (March 2021)

B. 5163. Triangle \(\displaystyle ABC\) is right-angled at \(\displaystyle C\). The right angle is divided \(\displaystyle 2:1\) by a line such that the smaller part is closer to the shorter leg. This line intersects hypotenuse \(\displaystyle AB\) at \(\displaystyle T\), and the circumscribed circle at \(\displaystyle D\). What are the measures of the acute angles of the triangle if the feet of the perpendiculars dropped from \(\displaystyle D\) onto the lines of the legs are collinear with \(\displaystyle T\)?

(4 pont)

Deadline expired on April 12, 2021.

Sorry, the solution is available only in Hungarian. Google translation

I. megoldás. Legyen a háromszög rövidebb befogója \(\displaystyle AC\).

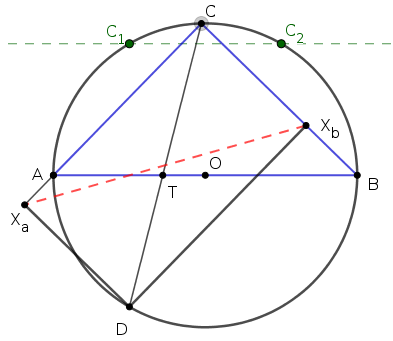
A háromszögben \(\displaystyle C\)-nél derékszög van, továbbá a \(\displaystyle D\) pontból merőlegeseket állítottunk a két befogóra, így a \(\displaystyle CX_aDX_b\) négyszög téglalap. A téglalap átlói felezik egymást, tehát a \(\displaystyle T\) pont akkor van rajta az \(\displaystyle X_aX_b\) egyenesen, ha \(\displaystyle T\) felezi a \(\displaystyle CD\) szakaszt. Ez azt jelenti, hogy ha a \(\displaystyle T\) pontot \(\displaystyle D\)-ből kétszeresére nagyítjuk, akkor a \(\displaystyle C\) pontba jutunk.

A kerületi és középponti szögek tétele miatt \(\displaystyle D\) a \(\displaystyle C\)-t nem tartalmazó \(\displaystyle AB\) ív \(\displaystyle A\)-hoz közelebbi harmadolópontja. Nagyítsuk \(\displaystyle D\)-ből kétszeresére az \(\displaystyle AB\) egyenest; ez kimetszi a körön a lehetséges \(\displaystyle C\) pontokat: a \(\displaystyle C_1\) a \(\displaystyle D\) tükörképe az \(\displaystyle AB\) átmérőre, a \(\displaystyle C_2\) pedig a \(\displaystyle D\) tükörképe a kör középpontjára, ezek a felső \(\displaystyle AB\) félkör harmadolópontjai.

A két metszéspont közül \(\displaystyle C_2\) nem megfelelő, mert \(\displaystyle AC_2>BC_2\). Tehát \(\displaystyle C=C_1\), \(\displaystyle CBA\angle=30^\circ\) és \(\displaystyle BAC\angle=60^\circ\).

II. megoldás. A szögek nagysága a Wallace-egyenesre történő hivatkozással gyorsan meghatározható. Az előző megoldás jelöléseivel, a feladat feltételei alapján az \(\displaystyle ABC\) háromszög körülírt körének \(\displaystyle D\) pontjából a két befogóra bocsátott merőlegesek talppontja \(\displaystyle X_a\) és \(\displaystyle X_b\). Az \(\displaystyle X_aX_b\) egyenes tehát a \(\displaystyle D\) ponthoz tartozó Wallace-egyenes. Ez az egyenes a harmadik \(\displaystyle AB\) oldalt a \(\displaystyle T\) pontban metszi. A tétel alapján ez a \(\displaystyle D\) pontból az \(\displaystyle AB\)-re bocsátott merőleges talppontja. A \(\displaystyle CD\) ezek szeerint merőleges az \(\displaystyle AB\) átmérőre, így \(\displaystyle ACD\sphericalangle=30^{\circ}\) miatt \(\displaystyle CAB\sphericalangle=60^{\circ}\) és \(\displaystyle ABC\sphericalangle=30^{\circ}\).

Statistics:

79 students sent a solution.
4 points:	70 students.
3 points:	6 students.
2 points:	2 students.
1 point:	1 student.

Problems in Mathematics of KöMaL, March 2021