 Problem B. 5171. (April 2021)
Problem B. 5171. (April 2021)
B. 5171. Let \(\displaystyle OLMN\) be a tetrahedron, and the vertices \(\displaystyle A\), \(\displaystyle B\) and \(\displaystyle C\) of another tetrahedron \(\displaystyle OABC\) lie on the rays \(\displaystyle OL\), \(\displaystyle OM\) and \(\displaystyle ON\), respectively. The centre of the inscribed circle of triangle \(\displaystyle LMN\) coincides with the centroid of triangle \(\displaystyle ABC\). Show that the volume of tetrahedron \(\displaystyle OLMN\) is greater than or equal to the volume of tetrahedron \(\displaystyle OABC\). On what condition will the volumes of the two tetrahedra be equal?
(From the British qualifying competition for the olympiad, 1980)
(5 pont)
Deadline expired on May 10, 2021.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Legyen az \(\displaystyle ABC\triangle\) súlypontja \(\displaystyle S\), az \(\displaystyle LMN\triangle\) beírt körének középpontja \(\displaystyle K\). Jelölje az \(\displaystyle \overrightarrow{OX}\) vektort \(\displaystyle \mathbf x\), ahol \(\displaystyle X\) az \(\displaystyle A\), \(\displaystyle B\), stb. pontok valamelyike. Az \(\displaystyle LMN\) háromszög oldalainak hossza legyen \(\displaystyle \lambda, \mu\) és \(\displaystyle \nu\) (rendre az \(\displaystyle L\), \(\displaystyle M\), és \(\displaystyle N\) csúcsokkal szemben).
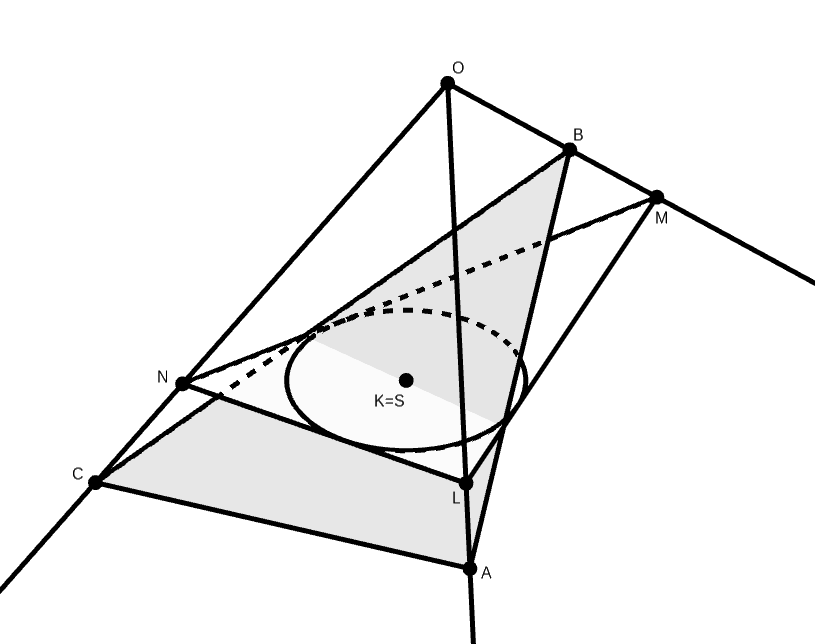
Az \(\displaystyle S\) súlypontba mutató vektorra \(\displaystyle \mathbf s=(\mathbf a+ \mathbf b+ \mathbf c)/3\), továbbá szintén jól ismert (egy levezetés található például itt, a 7. kidolgozott feladatban), hogy a \(\displaystyle K\) középpontba mutató vektorra
\(\displaystyle \mathbf k=\frac{\lambda}{\lambda+\mu +\nu}\mathbf l+\frac{\mu}{\lambda+\mu +\nu}\mathbf m + \frac{\nu}{\lambda+\mu +\nu}\mathbf n.\)
A feladat szövege szerint \(\displaystyle \mathbf s = \mathbf k\), így az \(\displaystyle \mathbf a \parallel \mathbf l\), \(\displaystyle \mathbf b \parallel \mathbf m\) és \(\displaystyle \mathbf c \parallel \mathbf n\) feltételek miatt
\(\displaystyle \frac{\mathbf a}{3}=\frac{\lambda}{\lambda+\mu +\nu}\mathbf l \, ; \, \frac{\mathbf b}{3}=\frac{\lambda}{\lambda+\mu +\nu}\mathbf m \, ; \, \frac{\mathbf c}{3}=\frac{\lambda}{\lambda+\mu +\nu}\mathbf n.\)
Ebből a vegyes szorzat tulajdonságai alapján
\(\displaystyle V_{OABC}=\frac{|\mathbf a \mathbf b \mathbf c|}{6}=\frac{3\lambda}{\lambda+\mu +\nu}\cdot \frac{3\mu}{\lambda+\mu +\nu}\cdot \frac{3\nu}{\lambda+\mu +\nu} \frac{|\mathbf l \mathbf m \mathbf n|}{6}=\frac{3\lambda}{\lambda+\mu +\nu}\cdot \frac{3\mu}{\lambda+\mu +\nu}\cdot \frac{3\nu}{\lambda+\mu +\nu} V_{OLMN},\)
azaz
\(\displaystyle V_{OABC}=\frac{27\lambda\mu \nu}{(\lambda+\mu+\nu)^3}V_{OLMN}.\)
A \(\displaystyle \lambda\), \(\displaystyle \mu\) és \(\displaystyle \nu\) pozitív számokra felírt számtani-mértani középegyenlőtlenség szerint
\(\displaystyle \frac{\lambda+\mu+\nu}{3}\ge \sqrt[3]{\lambda\mu\nu},\)
amiből átrendezéssel
\(\displaystyle \frac{27\lambda\mu \nu}{(\lambda+\mu+\nu)^3}\le 1.\)
Ebből \(\displaystyle V_{OABC}\le V_{OLMN}\) adódik, és egyenlőség csak \(\displaystyle \lambda=\mu=\nu\) esetben állhat, vagyis ha \(\displaystyle A=L\), \(\displaystyle B=M\) és \(\displaystyle C=N\) (továbbá \(\displaystyle ABC\triangle\) szabályos).
Statistics:
16 students sent a solution. 5 points: Diaconescu Tashi, Lovas Márton, Nádor Benedek, Simon László Bence, Sztranyák Gabriella, Varga Boldizsár. 4 points: Fekete Richárd, Koleszár Domonkos, Kökényesi Márk Péter, Mohay Lili Veronika, Nagy 551 Levente, Németh Márton, Seres-Szabó Márton. 2 points: 1 student. 0 point: 2 students.
Problems in Mathematics of KöMaL, April 2021
