A B. 5175. feladat (2021. május)

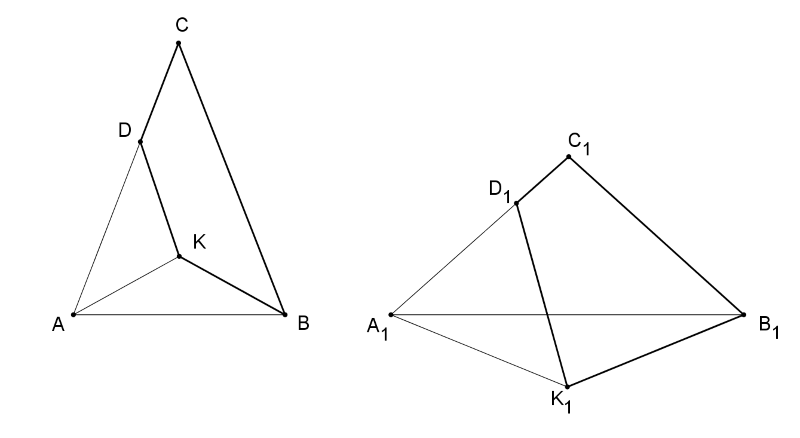
B. 5175. Az \(\displaystyle ABC\) háromszögben \(\displaystyle AC=BC\), az \(\displaystyle AC\) oldal egy belső pontja \(\displaystyle D\), az \(\displaystyle ABD\) kör középpontja \(\displaystyle K\). Mutassuk meg, hogy \(\displaystyle BCDK\) húrnégyszög.

(3 pont)

A beküldési határidő 2021. június 10-én LEJÁRT.

Megoldás. \(\displaystyle DAK\) és \(\displaystyle AKB\) egyenlő szárú háromszögek, azaz \(\displaystyle KD=KA=KB\), ezért

\(\displaystyle ADK\sphericalangle = KAD\sphericalangle , \ BAK\sphericalangle = KBA\sphericalangle. \)

Mivel a feltétel szerint \(\displaystyle ACB\) is egyenlőszárú, \(\displaystyle BAC\sphericalangle = CBA\sphericalangle\). Így – előjeles szögekkel számolva:

\(\displaystyle CBK\sphericalangle = CBA\sphericalangle - KBA\sphericalangle = BAC\sphericalangle - BAK\sphericalangle = KAD\sphericalangle = ADK\sphericalangle = 180^{\circ}-KDC \sphericalangle , \)

tehát \(\displaystyle BCDK\) valóban húrnégyszög.

Statisztika:

81 dolgozat érkezett.
3 pontot kapott:	62 versenyző.
2 pontot kapott:	16 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2021. májusi matematika feladatai