Problem B. 5177. (May 2021)

B. 5177. In a right-angled triangle \(\displaystyle ABC\), line segment \(\displaystyle CD\) is the altitude drawn to the hypotenuse. The circle \(\displaystyle k\) of diameter \(\displaystyle CD\) intersects the legs \(\displaystyle AC\) and \(\displaystyle BC\) again at points \(\displaystyle E\) and \(\displaystyle F\), respectively. The tangent drawn to circle \(\displaystyle k\) at point \(\displaystyle E\) intersects the line of leg \(\displaystyle BC\) at point \(\displaystyle P\), and the hypotenuse \(\displaystyle AB\) at point \(\displaystyle M\). The tangent drawn to circle \(\displaystyle k\) at point \(\displaystyle F\) intersects the line of leg \(\displaystyle AC\) at point \(\displaystyle Q\), and the hypotenuse \(\displaystyle AB\) at point \(\displaystyle N\). Prove that

\(\displaystyle 4\cdot MN^2=PE^2+QF^2+2\cdot EF^2. \)

(5 pont)

Deadline expired on June 10, 2021.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyenek az \(\displaystyle ABC\) háromszög oldalai és szögei a szokásosan jelölve, az ábra szerint.

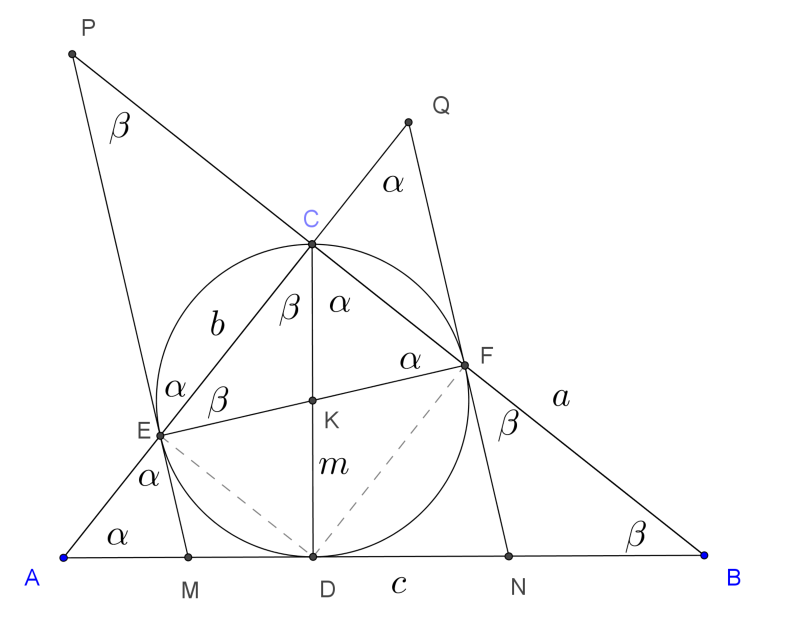
Az átfogóhoz tartozó magasság a háromszöget az eredetihez hasonló háromszögekre bontja, \(\displaystyle DCB\sphericalangle=CAB\sphericalangle=\alpha\) és \(\displaystyle ACD\sphericalangle=ABC\sphericalangle=\beta\).

A \(\displaystyle CD\) magasság Thalész-körének középpontja a \(\displaystyle K\) pont. A Thalész-kör a befogókat másodszor az \(\displaystyle E\) és \(\displaystyle F\) pontokban metszi, vagyis ezekből a pontokból a \(\displaystyle CD\) szakasz derékszögben látszik, másként fogalmazva a \(\displaystyle CEDF\) négyszög három szöge derékszög, a négyszög téglalap. Rögzíthetjük, hogy az \(\displaystyle EF\) szakasz szintén a kör átmérője, \(\displaystyle EF=CD=m\), továbbá az \(\displaystyle EF\) felezőpontja is a \(\displaystyle K\) pont. A téglalap-tulajdonságok miatt \(\displaystyle EKC\) és \(\displaystyle FKC\) egyenlő szárú háromszögek, így az eddigieket is figyelembe véve \(\displaystyle FEC\sphericalangle=\beta\) és \(\displaystyle EFC\sphericalangle=\alpha\). A Thalész-körhöz húzott érintők merőlegesek az érintési ponthoz tartozó átmérőre, következésképpen \(\displaystyle EPF\sphericalangle=\beta\) és \(\displaystyle FQE\sphericalangle=\alpha\).

Az \(\displaystyle ADC\) és \(\displaystyle QFE\) derékszögű háromszögek hegyesszögei \(\displaystyle \alpha\) és \(\displaystyle \beta\), továbbá az \(\displaystyle \alpha\) szöggel szemközti befogójuk is egyfoma hosszúságú: \(\displaystyle CD=EF=m\), tehát egybevágó háromszögek. Ugyanezzel a gondolatmenettel a \(\displaystyle BDC\) és \(\displaystyle PEF\) derékszögű háromszögek is egybevágók. Az egybevágóság és a Pitagorasz-tétel segítségével:

\(\displaystyle PE^2+EF^2+QF^2+EF^2=PF^2+QE^2=BC^2+CA^2=a^2+b^2=c^2.\)

A megoldás befejezéséhez tehát elegendő igazolni, hogy az \(\displaystyle MN\) szakasz az \(\displaystyle AB\) átfogó fele.

Az \(\displaystyle FEP\) derékszöget az \(\displaystyle EC\) magasság \(\displaystyle \beta\) és \(\displaystyle \alpha\) szögekre bontja. \(\displaystyle AEM\) és \(\displaystyle PEC\) csúcsszögek, \(\displaystyle PEC\sphericalangle=AEM\sphericalangle=EAM\sphericalangle=\alpha\), az \(\displaystyle AME\) háromszög egyenlő szárú. Másrészt az \(\displaystyle M\) pontból a \(\displaystyle CD\) Thalész-köréhez húzott érintőszakaszok is egyenlők, vagyis \(\displaystyle AM=EM=MD\), az \(\displaystyle MD\) szakasz az \(\displaystyle AD\) fele. Ugyanezzzel a módszerrel \(\displaystyle CFQ\) és \(\displaystyle NFB\) csúcsszögek, \(\displaystyle BNF\) egyenlő szárú háromszög, az \(\displaystyle N\) pontból húzott \(\displaystyle ND\) és \(\displaystyle NF\) érintőszakaszok is egyenlők, tehát \(\displaystyle ND\) a \(\displaystyle BD\) szakasz fele.

\(\displaystyle MN=MD+ND=\frac{AD}{2}+\frac{BD}{2}=\frac{AD+DB}{2}=\frac{c}{2}.\)

\(\displaystyle 4MN^2=c^2=a^2+b^2=PF^2+QE^2=PE^2+EF^2+QF^2+EF^2.\)

Statistics:

54 students sent a solution.
5 points:	Arató Zita, Bán-Szabó Áron, Baski Bence, Beinschroth Ninett, Bencsik Ádám, Bencsik Dávid, Benis Erzsébet, Bognár 171 András Károly, Csilling Dániel, Csizmadia Miklós, Diaconescu Tashi, Duchon Márton, Farkas 512 Izabella, Fekete Richárd, Fülöp Csilla, Hajdú Bálint, Hegedűs Dániel, Kalocsai Zoltán, Kercsó-Molnár Anita, Koleszár Domonkos, Kovács 129 Tamás, Kökényesi Márk Péter, Köpenczei Csanád, Lovas Márton, Mohay Lili Veronika, Molnár-Szabó Vilmos, Móricz Benjámin, Nádor Artúr, Nádor Benedek, Nagy 551 Levente, Németh Márton, Páhán Anita Dalma, Romaniuc Albert-Iulian, Seres-Szabó Márton, Simon László Bence, Sipeki Márton, Somogyi Dalma, Sztranyák Gabriella, Terjék András József, Török Ágoston, Trombitás Karolina Sarolta, Varga Boldizsár, Velich Nóra, Viharos Márta Judit, Virág Rudolf, Wiener Anna.
4 points:	Osztényi József, Udvardy Kata, Zömbik Barnabás.
3 points:	2 students.
2 points:	1 student.
1 point:	1 student.
Unfair, not evaluated:	1 solutions.

Problems in Mathematics of KöMaL, May 2021