A B. 5178. feladat (2021. május)

B. 5178. Legyen \(\displaystyle x\) pozitív valós szám. Mutassuk meg, hogy

\(\displaystyle \sqrt{6x+9}+\sqrt{16x+64}\le \left(\sqrt{x}+\frac{3}{\sqrt{x}}\right) \left(\sqrt{x}+\frac{8}{\sqrt{x}}\right). \)

Javasolta: Szoldatics József (Budapest)

(4 pont)

A beküldési határidő 2021. június 10-én LEJÁRT.

Megoldás. Legyen az egyenlőtlenség két oldala \(\displaystyle f(x)=\sqrt{6x+9}+\sqrt{16x+64}\) és \(\displaystyle g(x)=\Big(\sqrt{x}+\dfrac{3}{\sqrt{x}}\Big)\Big(\sqrt{x}+\dfrac{8}{\sqrt{x}}\Big)=x+11+\dfrac{24}x\); azt kell igazolnunk, hogy \(\displaystyle f(x)\le g(x)\). A megoldás azon fog múlni, hogy \(\displaystyle f(x)\) szigorúan konkáv, míg \(\displaystyle g(x)\) szigorúan konvex, és a két függvény grafikonjának van egy közös érintője; a közös érintő egyenletét \(\displaystyle y=t(x)\) alakban fogjuk felírni.

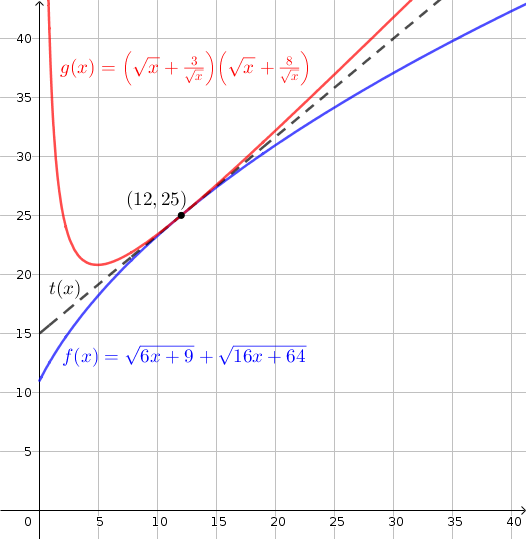
Próbálgatással kitalálható, hogy \(\displaystyle x=12\) esetén egyenlőség áll fenn, mert \(\displaystyle f(12)=\sqrt{81}+\sqrt{256}=25\) és \(\displaystyle g(12)=12+11+2=25\), tehát \(\displaystyle f(12)=g(12)=25\).

Az \(\displaystyle x=12\) pontban a két függvény meredeksége is megegyezik, mert

\(\displaystyle f'(x)=\dfrac{3}{\sqrt{6x+9}}+\dfrac{8}{\sqrt{16x+64}}, \qquad f'(12)=\dfrac{3}{\sqrt{6\cdot12+9}}+\dfrac{8}{\sqrt{16\cdot12+64}} = \dfrac56 \)

és

\(\displaystyle g'(x) = 1-\dfrac{24}{x^2}, \qquad g'(12) = 1-\dfrac{24}{12^2} = \dfrac56. \)

Tehát a \(\displaystyle (12,25)\) ponton átmenő, \(\displaystyle \dfrac56\) meredekségű egyenes, amelynek egyenlete \(\displaystyle y=t(x)=\dfrac56(x-12)+25\), a két függvény grafikonjának közös érintője.

Az \(\displaystyle f(x)\) konkávitása azonnal következik a \(\displaystyle \sqrt{x}\) függvény konkávitásából, míg \(\displaystyle g(x)\) konvexitása következik \(\displaystyle \dfrac1x\) konvexitásából, de a második derivált előjeléből is leolvashatjuk:

\(\displaystyle f''(x) = -\frac{9}{(6x+9)^{3/2}}-\frac{64}{(16x+64)^{3/2}} <0, \)

illetve

\(\displaystyle g''(x) = \frac{48}{x^3}>0. \)

Az \(\displaystyle f(x)\) szigorú konkávitása és a \(\displaystyle g(x)\) szigorú konvexitása miatt

\(\displaystyle f(x) \le t(x) \le g(x), \)

és mindkét oldalon csak az érintési pontban, vagyis \(\displaystyle x=12\) esetén áll egyenlőség.

Megjegyzés. A megoldást átírhatjuk úgy, hogy – legalábbis látszólag – ne használja a differenciálszámítás eszközeit:

\(\displaystyle \sqrt{6x+9} \le \sqrt{6x+9} + \frac1{18}\Big(\sqrt{6x+9}-9\Big)^2 = \frac{x}3+5; \)

\(\displaystyle \sqrt{16x+64} \le \sqrt{16x+64} + \frac1{32}\Big(\sqrt{16x+64}-16\Big)^2 = \frac{x}2+10; \)

\(\displaystyle \frac{x}{6}+\dfrac{24}x \ge 2 \sqrt{\frac{x}{6}\cdot\dfrac{24}x} = 4; \)

\(\displaystyle \sqrt{6x+9} + \sqrt{16x+64} \le \Big(\frac{x}3+5\Big)+\Big(\frac{x}2+10\Big) = \Big(\dfrac56x+11\Big)+4 \le \Big(\dfrac56x+11\Big)+\Big(\frac{x}6+\dfrac{24}x\Big) \le x+11+\dfrac{24}x. \)

Statisztika:

52 dolgozat érkezett.
4 pontot kapott:	Arató Zita, Bán-Szabó Áron, Barta Zsófia, Baski Bence, Ben Gillott, Bencsik Ádám, Bencsik Dávid, Bognár 171 András Károly, Csizmadia Miklós, Csonka Illés, Diaconescu Tashi, Duchon Márton, Farkas 512 Izabella, Fekete Richárd, Hajdú Bálint, Hegedűs Dániel, Horváth 530 Mihály, Horváth Áron, Kalocsai Zoltán, Kercsó-Molnár Anita, Koleszár Domonkos, Kökényesi Márk Péter, Köpenczei Csanád, Mácsai Dániel, Metzger Ábris András, Molnár-Szabó Vilmos, Móricz Benjámin, Nádor Artúr, Nádor Benedek, Nagy 551 Levente, Németh Márton, Nyárfádi Patrik, Páhán Anita Dalma, Richlik Bence, Romaniuc Albert-Iulian, Seres-Szabó Márton, Simon László Bence, Somogyi Dalma, Szakács Ábel, Szanyi Attila, Terjék András József, Tóth 057 Bálint, Varga Boldizsár, Velich Nóra, Viharos Márta Judit, Zömbik Barnabás.
3 pontot kapott:	5 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2021. májusi matematika feladatai