 Problem B. 5180. (May 2021)
Problem B. 5180. (May 2021)
B. 5180. The radius of the circumscribed circle of a regular heptagon \(\displaystyle ABCDEFG\) is \(\displaystyle r\). Prove that the circle of radius \(\displaystyle 2r\) centred at \(\displaystyle A\) passes through the orthocentre of triangle \(\displaystyle BCE\).
(5 pont)
Deadline expired on June 10, 2021.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Legyen a hétszög középpontja \(\displaystyle O\), a \(\displaystyle BCE\) háromszög magasságpontja \(\displaystyle M\). Azt kell igazolnunk, hogy \(\displaystyle AM=2r\).
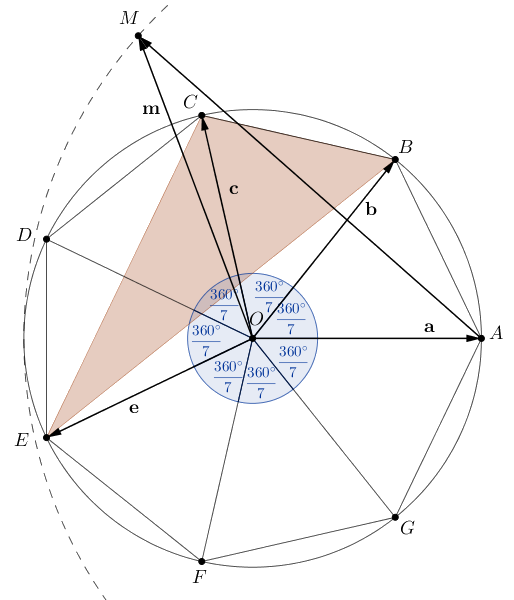
Legyen
\(\displaystyle \mathbf{a}=\overrightarrow{OA}, \quad \mathbf{b}=\overrightarrow{OB}, \quad \mathbf{c}=\overrightarrow{OC}, \quad \mathbf{e}=\overrightarrow{OE} \quad \text{és} \quad \mathbf{m}=\overrightarrow{OM}. \)
A hétszög köré írt kör középontja \(\displaystyle O\), ezért
\(\displaystyle |\mathbf{a}|=|\mathbf{b}|=|\mathbf{c}|=|\mathbf{e}|=r. \)
Az \(\displaystyle O\) pont egyben a \(\displaystyle BCE\) háromszög köré írt kör középontja is, ezért
\(\displaystyle \mathbf{m} = \overrightarrow{OM} = \overrightarrow{OB} +\overrightarrow{OC} +\overrightarrow{OE} = \mathbf{b}+\mathbf{c}+\mathbf{e}, \)
tehát
\(\displaystyle \overrightarrow{AM} = \overrightarrow{OM}-\overrightarrow{OA} = (\mathbf{b}+\mathbf{c}+\mathbf{e}) -\mathbf{a}. \)
Emeljük négyzetre skalárisan az \(\displaystyle \overrightarrow{AM}\) vektort:
$$\begin{align*} AM^2 &= \Big(\overrightarrow{AM}\Big)^2 = (\mathbf{b}+\mathbf{c}+\mathbf{e}-\mathbf{a})^2 = \mathbf{b}^2+\mathbf{c}^2+\mathbf{e}^2+\mathbf{a}^2 +2\mathbf{b}\mathbf{c} +2\mathbf{b}\mathbf{e} +2\mathbf{c}\mathbf{e} -2\mathbf{a}\mathbf{b} -2\mathbf{a}\mathbf{c} -2\mathbf{a}\mathbf{e}= \\ &= 4r^2 +2(\mathbf{b}\mathbf{c}-\mathbf{a}\mathbf{b}) +2(\mathbf{c}\mathbf{e}-\mathbf{a}\mathbf{c}) +2(\mathbf{b}\mathbf{e}-\mathbf{a}\mathbf{e}). \tag{*} \end{align*}$$Vegyük észre, hogy \(\displaystyle AOB\sphericalangle=BOC\sphericalangle=\frac{360^\circ}{7}\) miatt \(\displaystyle \mathbf{a}\mathbf{b}=\mathbf{b}\mathbf{c}\), \(\displaystyle AOC\sphericalangle=COE\sphericalangle=\frac{2\cdot360^\circ}{7}\) miatt \(\displaystyle \mathbf{a}\mathbf{c}=\mathbf{c}\mathbf{e}\), és ugyanígy \(\displaystyle EOA\sphericalangle=BOE\sphericalangle=\frac{3\cdot360^\circ}{7}\) miatt \(\displaystyle \mathbf{a}\mathbf{e}=\mathbf{b}\mathbf{e}\). A \(\displaystyle (*)\) jobboldalán ezek a tagok mind kiesnek, ezzel azt kapjuk, hogy
\(\displaystyle AM^2 = 4r^2, \)
vagyis
\(\displaystyle AM = 2r, \)
és éppen ezt kellett igazolni.
Statistics:
33 students sent a solution. 5 points: Arató Zita, Bán-Szabó Áron, Baski Bence, Csonka Illés, Diaconescu Tashi, Dienes Ervin Fotisz, Fekete Richárd, Hegedűs Dániel, Kalocsai Zoltán, Kercsó-Molnár Anita, Koleszár Domonkos, Lovas Márton, Mohay Lili Veronika, Móricz Benjámin, Nádor Benedek, Nagy 551 Levente, Németh Márton, Osztényi József, Romaniuc Albert-Iulian, Seres-Szabó Márton, Simon László Bence, Somogyi Dalma, Sztranyák Gabriella, Török Ágoston, Wiener Anna, Zömbik Barnabás. 4 points: Beinschroth Ninett, Csizmadia Miklós, Molnár-Szabó Vilmos. 3 points: 1 student. 2 points: 1 student. 1 point: 2 students.
Problems in Mathematics of KöMaL, May 2021
