A B. 5181. feladat (2021. május)

B. 5181. Adott a síkon nyolc pont, melyek közül semelyik három nem esik egy egyenesre és semelyik öt nincs egy körön. Legfeljebb hány olyan kör lehet, mely az adott pontok közül négyre illeszkedik?

Javasolta: Imolay András (Budapest)

(6 pont)

A beküldési határidő 2021. június 10-én LEJÁRT.

Megoldás. Legfeljebb \(\displaystyle 12\) ilyen kör lehet.

Konstrukció. \(\displaystyle 8\) pont között \(\displaystyle 10\) húrnégyszöget könnyű találni, ha az \(\displaystyle A,B,C,D,E,F,G\) és \(\displaystyle H\) pontokat az ábrán látható elrendezésben helyezzük el.

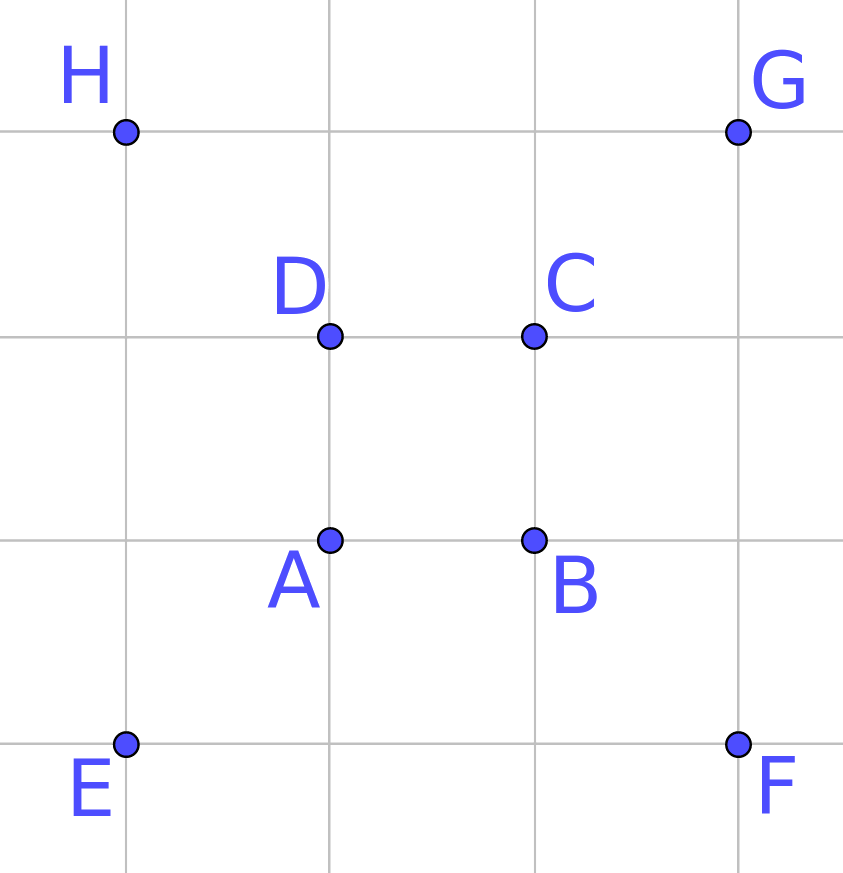
Az ábrán \(\displaystyle ABCD\) és \(\displaystyle EFGH\) két párhuzamos állású és azonos középpontú téglalap. Ekkor ezen két négyzet mellett még 8 húrtrapéz is van az ábrán (\(\displaystyle ABFE\) és 3 elforgatottja, illetve \(\displaystyle ABGH\) és 3 elforgatottja). Nincsen 5 pont egy körön. Hiszen ha lenne, akkor közülük vagy legalább 3 az \(\displaystyle ABCD\) négyzet csúcsai közül kerülne ki, vagy legalább 3 az \(\displaystyle EFGH\) négyzet csúcsai közül. Ez a 3 pont pedig már egyértelműen meghatározná valamelyik négyzet körülírt körét. Márpedig egyik négyzet körülírt körén sincs ötödik pont.

Van viszont két egyenes is, amely 4 pontot is tartalmaz (\(\displaystyle E,A,C,G\)) és (\(\displaystyle H,D,B,F\)). Tehát nem is teljeseítettük a feladat összes feltételét. Viszont ha ezekből az egyenesekből ,,kört tudnánk csinálni'', akkor ez a gond megoldódna, ráadásul két újabb húrnégyszöget kapnánk.

Hogyan csináljunk egyenesekből kört? Erre való az inverzió. Az inverzió középpontjául egy olyan \(\displaystyle P\) pontot válasszunk, amely nincsen rajta a \(\displaystyle 8\) pont közül semely \(\displaystyle 2\)-nek az egyenesén, és semely \(\displaystyle 3\)-nak a körülírt körén.

Az inverzió tulajdonságai miatt ekkor az eredeti 10 húrnégyszög megmarad húrnégyszögnek, és a két 4-pontú egyenesből is egy-egy húrnégyszög lesz. 5 pont nem lesz egy körön az inverzió után sem, hiszen akkor az inverzió előtt is egy körön vagy egy egyenesen kellett volna lennie ennek az 5 pontnak. És semely 3 pont nem lesz egy egyenesen, mert ahhoz az inverzió középpontjával közös körön kellett volna lenniük eredetileg.

Felső becslés. Indirekten tegyük fel, hogy valaki megadott 8 pontot a feltételeknek megfelelően (nincs 5 egy körön, nincs 3 egy egyenesen), melyek legalább \(\displaystyle 13\) húrnégyszöget határoznak meg.

Ha minden ponton legfeljebb \(\displaystyle 6\) ilyen kör menne át, akkor összesen legfeljebb \(\displaystyle \frac{6 \cdot 8}{4}=12\) kör lenne, így a nyolc pont között van egy (nevezzük \(\displaystyle H\)-nak), amely legalább \(\displaystyle 7\) húrnégyszögnek csúcsa.

Most alkalmazzunk egy \(\displaystyle H\) középpontú inverziót, a másik 7 pont képét pedig fessük kékre. A \(\displaystyle H\)-t tartalmazó húrnégyszögeket az inverzió olyan egyenesekbe viszi, amelyek a kék pontok közül pontosan 3-at tartalmaznak. Ezt a 7 egyenest színezzük pirosra (ha több, mint 7 ilyen egyenes lenne, akkor tetszőleges 7-et fessünk közülünk pirosra).

A következőkben belátjuk, hogy a 7 kék pont a 7 piros egyenessel egy szép, szimmetikus konfigurációt alkot (melynek neve Fano-sík).

Ehhez először bebizonyítjuk, hogy a 7 kék pont mindegyikén pontosan 3 piros egyenes megy át.

(i) Egyrészt, 3-nál több nem mehet át egy kék ponton. Ha ugyanis rögzítünk egy \(\displaystyle K\) kék pontot, akkor a maradék 6 kék pont közül diszjunkt párokat kell tartalmazzon egy-egy \(\displaystyle K\)-n átmenő egyenes.

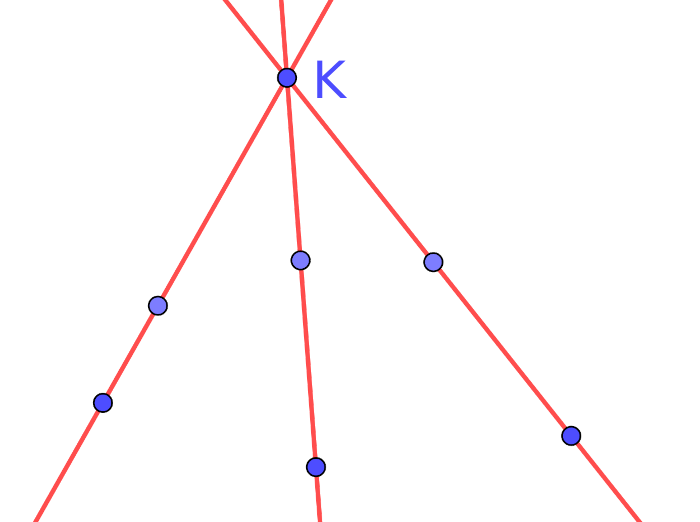
(ii) Másrészt, az egy kék ponton átmenő piros egyenesek száma átlagosan: \(\displaystyle \frac{7 \cdot 3}{7} = 3\), hiszen 7 piros egyenesünk van, és mindegyik 3 kék ponton megy át.

Ez a kettő egyszerre csak akkor teljesülhet, ha minden kék ponton pontosan 3 piros egyenes megy át. De az (i)-ben leírtakból így az is következik, hogy bármely két kék pontot pontosan egy piros egyenes köt össze.

Most válasszunk ki 3 kék pontot, amelyek nem esnek egy piros egyenesre, ezeket nevezzük el \(\displaystyle A,B,C\)-nek. A \(\displaystyle B\)-t és \(\displaystyle C\)-t összekötő piros egyenesen a harmadik kék pont legyen \(\displaystyle D\); a \(\displaystyle C\)-t és az \(\displaystyle A\)-t összekötő piros egyenesen a harmadik kék pont legyen \(\displaystyle E\); míg az \(\displaystyle A\)-t és \(\displaystyle B\)-t összekötő piros egyenes harmadik kék pontja legyen \(\displaystyle F\).

Az \(\displaystyle A\)-t és \(\displaystyle D\)-t is össze kell kösse egy piros egyenes, ezen is kell legyen egy harmadik kék pont. Ez nem lehet \(\displaystyle B,C,E,F\) egyike sem (hiszen az \(\displaystyle A\)-t ezekkel összekötő piros egyeneseknek már ismerjük mindhárom kék pontját). Tehát ez csak a hetedik kék pont lehet, nevezzük \(\displaystyle G\)-nek. Hasonló gondolatmenettel beláthatjuk, hogy a \(\displaystyle (B,E,G)\) és a \(\displaystyle (C,F,G)\) ponthármasok is egy egyenesre esnek.

(Egy-egy piros egyenesen belül a kék pontok sorrendje többféle is lehet, a sok közül két lehetséges esetet mutatnak az alábbi ábrák:)

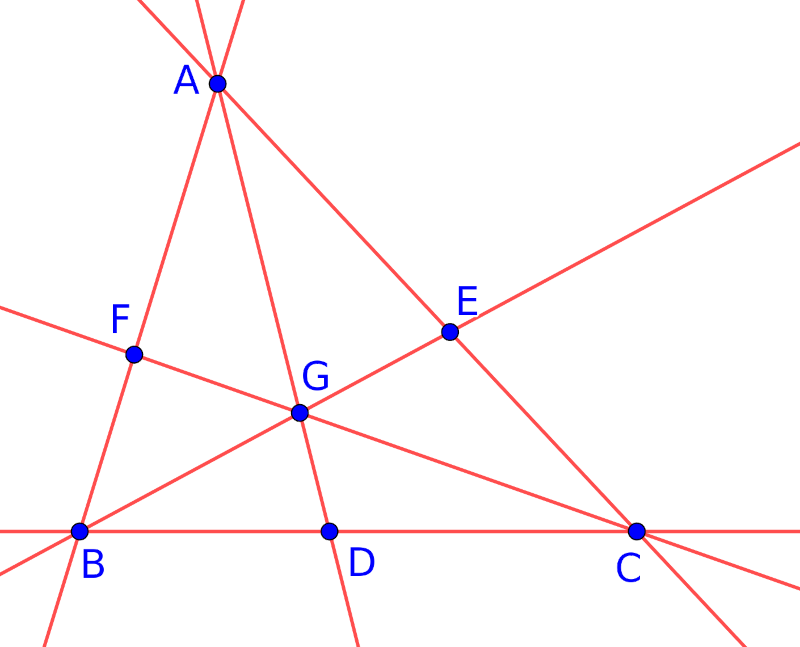\(\displaystyle \quad\)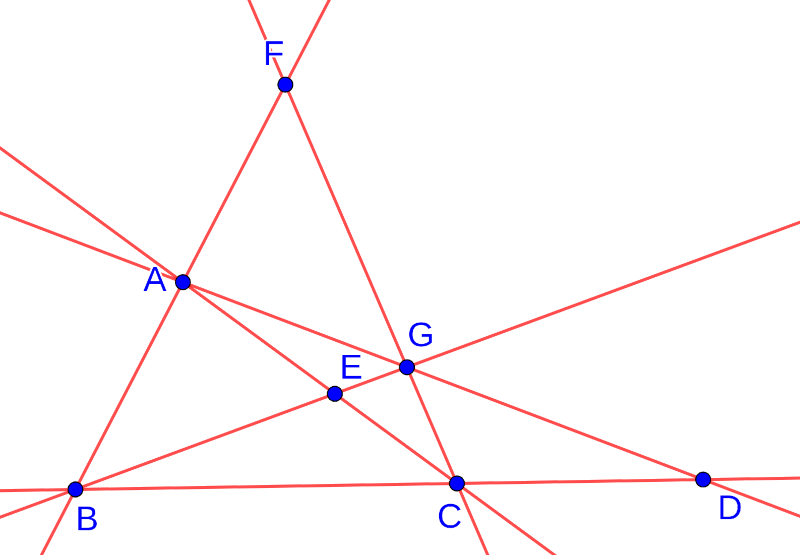

Ezzel már 6 egyenest találtunk. 3 olyan kék pont van, amely eddig csak 2 piros egyenesen van rajta: \(\displaystyle D,E,F\). Tehát nekik kell alkotniuk a hetedik piros egyenest.

Ezzel feltérképeztük a piros egyenesek és a kék pontok illeszkedési viszonyait (beláttuk, hogy Fano-síkot alkotnak). Fano axiómája néven is ismert az az állítás, hogy 7 pont és 7 egyenes között ilyen illeszkedések nem valósíthatóak meg az euklideszi síkon (és a valós projektív síkon sem). Mivel ezt a tényt sok helyen kimondják (néha ebben a formában: egy teljes négyoldal három átlós pontja nem eshet egy egyenesre), de kevés helyen bizonyítják, ezért adunk erre is egy indoklást.

Vizsgáljuk meg a \(\displaystyle G\) pontnak a helyzetét az \(\displaystyle ABC\) háromszöghöz képest. Bebizonyítjuk, hogy akárhol is van \(\displaystyle G\), a \(\displaystyle D,E,F\) pontok közül 1 vagy 3 fog az \(\displaystyle ABC\) oldalainak belsejében elhelyezkedni. Ezzel pedig ellentmondáshoz jutunk, mivel egy háromszögvonalat csak 0 vagy 2 pontban metszhet egy olyan egyenes, amely nem megy át a háromszög egyik csúcsán sem (ez az ún. Pasch-axióma).

Az \(\displaystyle ABC\) háromszög oldalegyenesei a sík háromszögön kívüli részét 6 tartományra vágják, ezeket az ábrán látható módon elnevezzük \(\displaystyle T_1,T_2,\ldots,T_6\) tartományoknak.

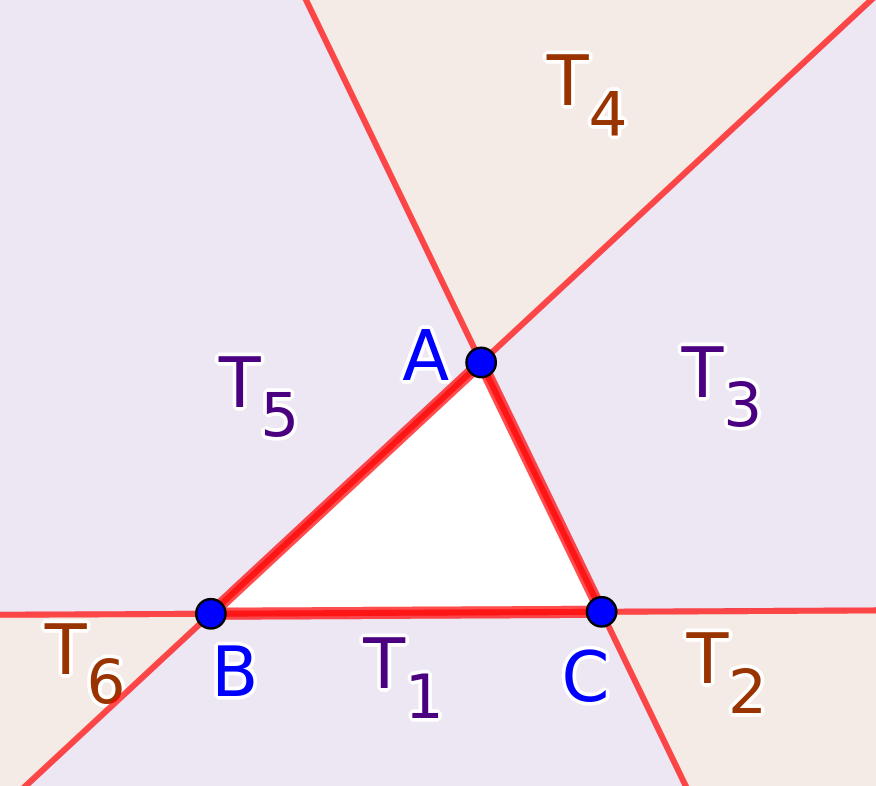
• Ha \(\displaystyle G\) a háromszög belsejében van, akkor \(\displaystyle D\), \(\displaystyle E\) és \(\displaystyle F\) is a háromszög oldalszakaszain belül fog elhelyezkedni.
• Ha \(\displaystyle G\) a \(\displaystyle T_1\) tartományban van, akkor \(\displaystyle D\) a háromszög \(\displaystyle BC\) oldalán belül lesz, míg \(\displaystyle E\) és \(\displaystyle F\) a megfelelő oldalakon kívül. Ugyanígy kezelhető a \(\displaystyle T_3\) és a \(\displaystyle T_5\) tartomány.
• Ha \(\displaystyle G\) a \(\displaystyle T_2\) tartományban van, akkor \(\displaystyle D\) és \(\displaystyle E\) kívül lesz a háromszög oldalszakaszain, míg \(\displaystyle F\) belül. Ugyanígy kezelhető a \(\displaystyle T_4\) és \(\displaystyle T_6\) tartomány.

Ezzel bebizonyítottuk, hogy nem keletkezhet 12-nél több húrnégyszög, ha a feltételeknek megfelelően helyezzük el a 8 pontot.

Statisztika:

24 dolgozat érkezett.
6 pontot kapott:	Bán-Szabó Áron, Fekete Richárd, Kalocsai Zoltán, Kercsó-Molnár Anita, Koleszár Domonkos, Nádor Benedek, Nagy 551 Levente, Seres-Szabó Márton, Somogyi Dalma, Sztranyák Gabriella, Terjék András József, Varga Boldizsár.
4 pontot kapott:	2 versenyző.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	4 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2021. májusi matematika feladatai