 |
A B. 5184. feladat (2021. szeptember) |
B. 5184. Kornélia felvett a síkon négy pontot úgy, hogy ne essenek egy körre. Ezután megrajzolta az összes körvonalat, amely ettől a négy ponttól egyenlő távolságra halad el. Legfeljebb hány kört rajzolhatott? (Az \(\displaystyle O\) középpontú \(\displaystyle k\) körvonal és a \(\displaystyle P\) pont távolsága így mérendő: az \(\displaystyle O\)-ból induló \(\displaystyle P\)-t tartalmazó félegyenes és a \(\displaystyle k\) körvonal metszéspontja legyen \(\displaystyle M\). Ekkor a \(\displaystyle PM\) szakasz hossza lesz a keresett távolság.)
(5 pont)
A beküldési határidő 2021. október 11-én LEJÁRT.
Megoldás. Jelölje \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\) a Kornélia által felvett pontokat. Vizsgáljuk meg, milyen lehet egy jó (azaz a feladat feltételeinek eleget tevő) \(\displaystyle k\) kör. Jelöljük \(\displaystyle O\)-val a középpontját, \(\displaystyle r\)-rel a sugarát és \(\displaystyle d\)-vel a négy ponttól vett közös távolságát. Bonstunk esetekre aszerint, hogy az \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\) pontok közül hány esik a \(\displaystyle k\) körön belülre, illetve kívülre.
(4:0) Az nem lehetséges, hogy mind a 4 pont belülre esik, mivel akkor \(\displaystyle OA = OB = OC = OD = r-d\) lenne, azaz mind az \(\displaystyle O\) középpontú, \(\displaystyle r-d\) sugarú körre esnének. Hasonlóképp nem lehet mind a 4 pont kívül sem.
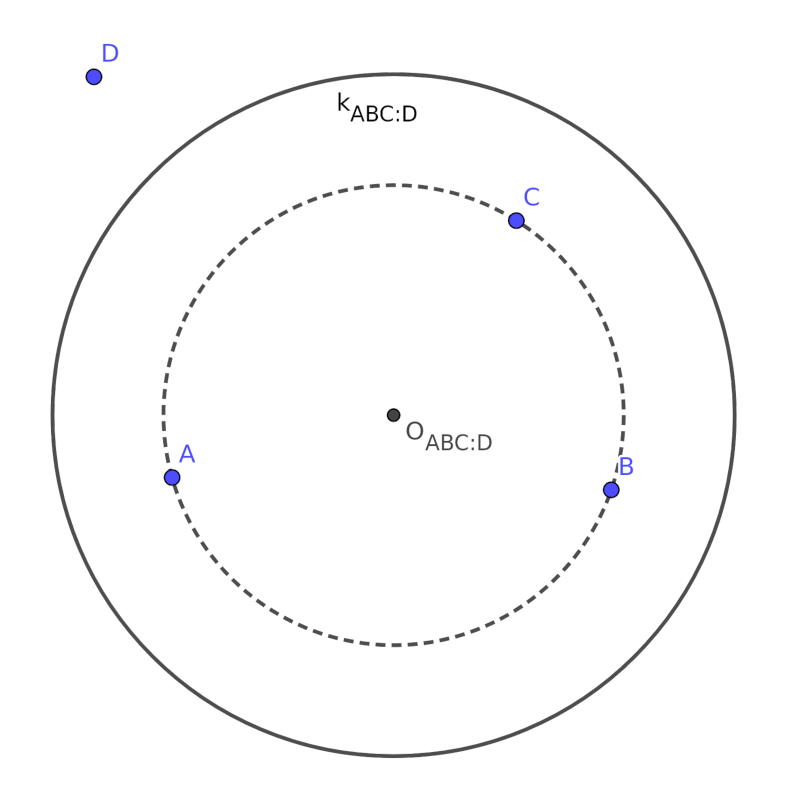
(3:1) Ha \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\) belülre, míg \(\displaystyle D\) kívülre esik, akkor teljesül, hogy \(\displaystyle OA = OB = OC = r-d\), tehát \(\displaystyle O\)-nak az \(\displaystyle ABC\) háromszög körülírt körének középpontjában kell lennie (ha \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) egy egyenesre esik, akkor nem lehet ilyen kör). Mivel \(\displaystyle OD = r+d\), ezért \(\displaystyle r = \frac{OA+OD}{2}\), tehát a kör sugarát is egyértelműen meghatároztuk.
Sőt, ha olyan \(\displaystyle k\) jó kört keresnénk, amelyhez képest \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) esik kívülre és \(\displaystyle D\) belülre, akkor megint azt kapnánk, hogy \(\displaystyle O\)-nak az \(\displaystyle ABC\) háromszög körülírt körének középpontjában kell lennie, míg az \(\displaystyle r\) sugárra most is teljesül \(\displaystyle r = \frac{OA+OD}{2}\) (hiszen ezúttal \(\displaystyle OA=OB=OC=r-d\) és \(\displaystyle OD=r+d\)). Tehát a kétfajta körből csak az egyik létezhet, és az is egyértelműen megszerkeszthető.
Tehát legfeljebb egy olyan kör lehet, amely \(\displaystyle D\)-t különválasztja az \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) pontoktól. És így összesen legfeljebb 4 jó kör lehet, amely 1 pontot választ külön a másik háromtól (röviden: \(\displaystyle (3:1)\)-típusú).
 \(\displaystyle \qquad\) \(\displaystyle \qquad\) \(\displaystyle \qquad\) \(\displaystyle \qquad\)
\(\displaystyle \qquad\) \(\displaystyle \qquad\) \(\displaystyle \qquad\) \(\displaystyle \qquad\) 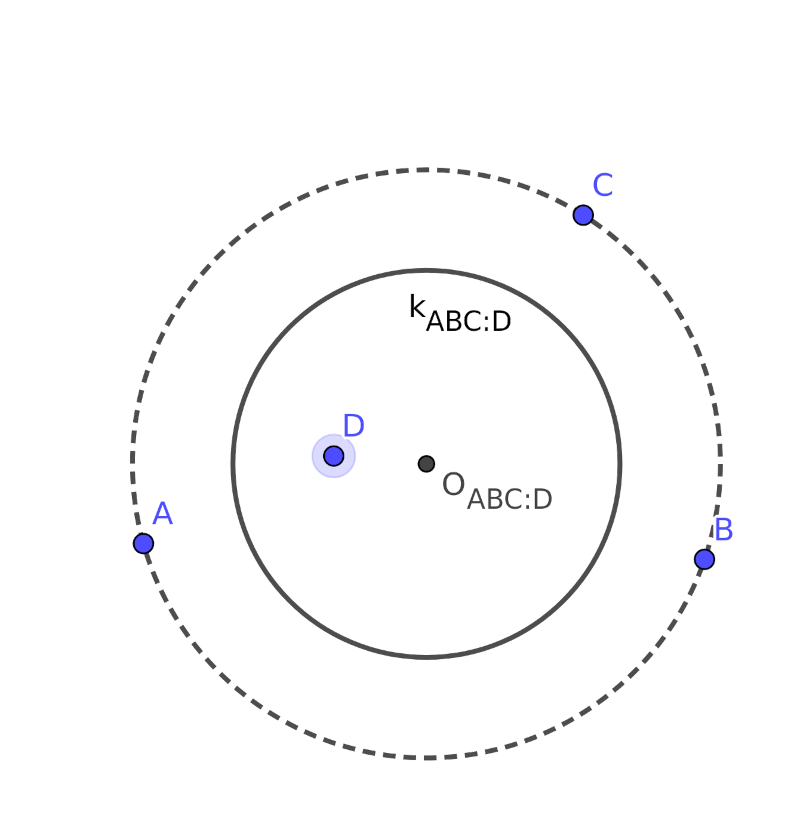
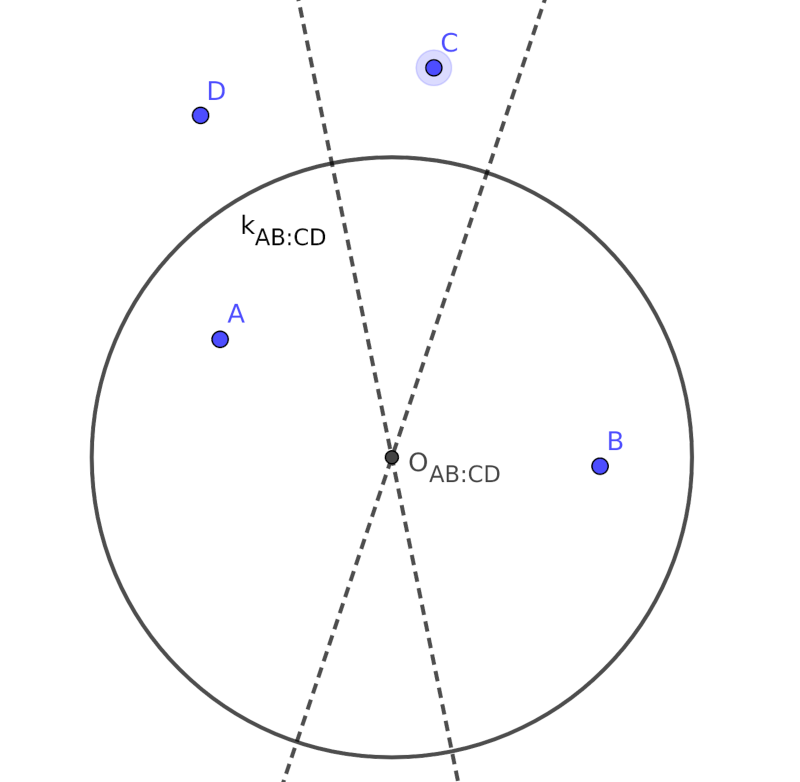
(2:2) Ha \(\displaystyle A\) és \(\displaystyle B\) belülre, míg \(\displaystyle C\) = \(\displaystyle D\) kívülre esik, akkor \(\displaystyle OA=OB=r-d\) és \(\displaystyle OC=OD=r+d\); tehát \(\displaystyle O\)-nak rajta kell lennie az \(\displaystyle AB\) és a \(\displaystyle CD\) szakaszok felezőmerőlegesén is. Ha ez a két felezőmerőleges egybeesne, akkor \(\displaystyle ABCD\) szimmetrikus trapézt, azaz húrnégyszöget alkotna, amit kizárnak a feladat feltételei. Tehát a két felezőmerőlegesnek legfeljebb egy közös pontja lehet, ez lesz \(\displaystyle O\). Az \(\displaystyle r\) sugárra megint felírhatjuk, hogy \(\displaystyle r = \frac{OA+OD}{2}\).
Ha olyan jó kört keresnénk, amelyhez képest \(\displaystyle A\) és \(\displaystyle B\) kerül kívülre, míg \(\displaystyle C\) és \(\displaystyle D\) belülre, akkor ugyanezt az \(\displaystyle O\)-t és \(\displaystyle r\)-t kapnánk. Tehát ebből a kétfajta is csak az egyik létezhet, és az is egyértelműen megszerkeszthető.
 \(\displaystyle \qquad\) \(\displaystyle \qquad\) \(\displaystyle \qquad\) \(\displaystyle \qquad\)
\(\displaystyle \qquad\) \(\displaystyle \qquad\) \(\displaystyle \qquad\) \(\displaystyle \qquad\) 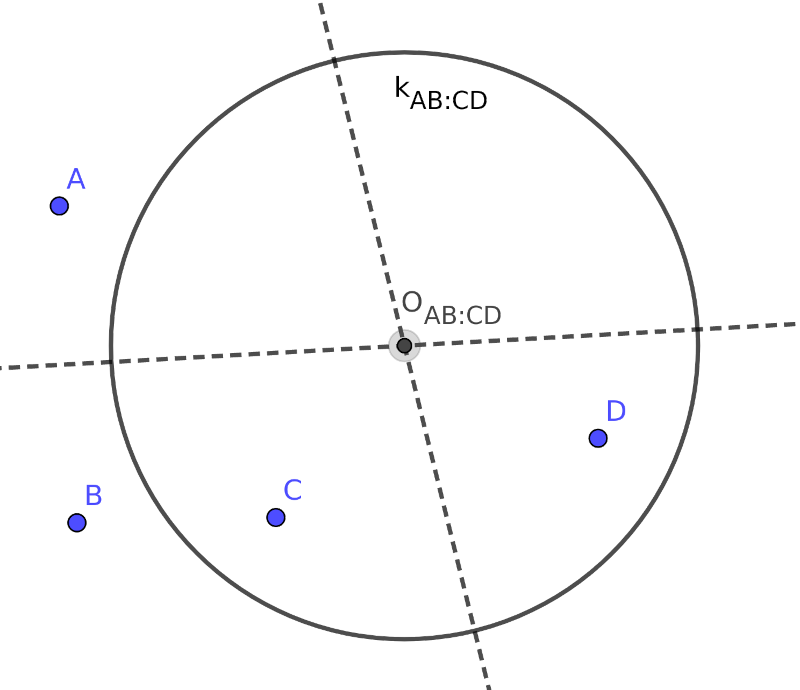
Azaz legfeljebb egy olyan kör lehet, amely \(\displaystyle A\)-t és \(\displaystyle B\)-t különválasztja \(\displaystyle C\)-től és \(\displaystyle D\)-től. Mivel 4 pontot 3-féleképpen tudunk két párra szétválasztani, így legfeljebb 3 darab \(\displaystyle (2:2)\)-típusú jó kör lehet.
Ezzel beláttuk, hogy a jó körök számának felső korlátja \(\displaystyle 4+3=7\).
7 jó kör pedig tényleg meg is valósítható. Gondoljuk végig, hogy minek kell ehhez teljesülni:
- \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\) közül semely három nem eshet egy egyenesre. Ekkor közülük bármely háromnak van körülírt köre, ennek középpontjával találunk egy jó \(\displaystyle (3:1)\)-típusú kört.
- \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\) nem lehetnek egy trapéz csúcsai. Ekkor a páronként vett felezőmerőlegeseik között nem lesz párhuzamos pár, azaz minden \(\displaystyle (2:2)\)-típusú jelöltnek megtaláljuk a középpontját két felezőmerőleges egyetlen metszéspontjaként.
Ha ez a két feltétel egyszerre teljesül, akkor mind a 7 esetben meg tudunk szerkeszteni egy-egy jó kört. Az pedig világos, hogy ez a 7 jó kör tényleg különböző, hiszen egyenként eltérő módon vágják szét a négy pontot.
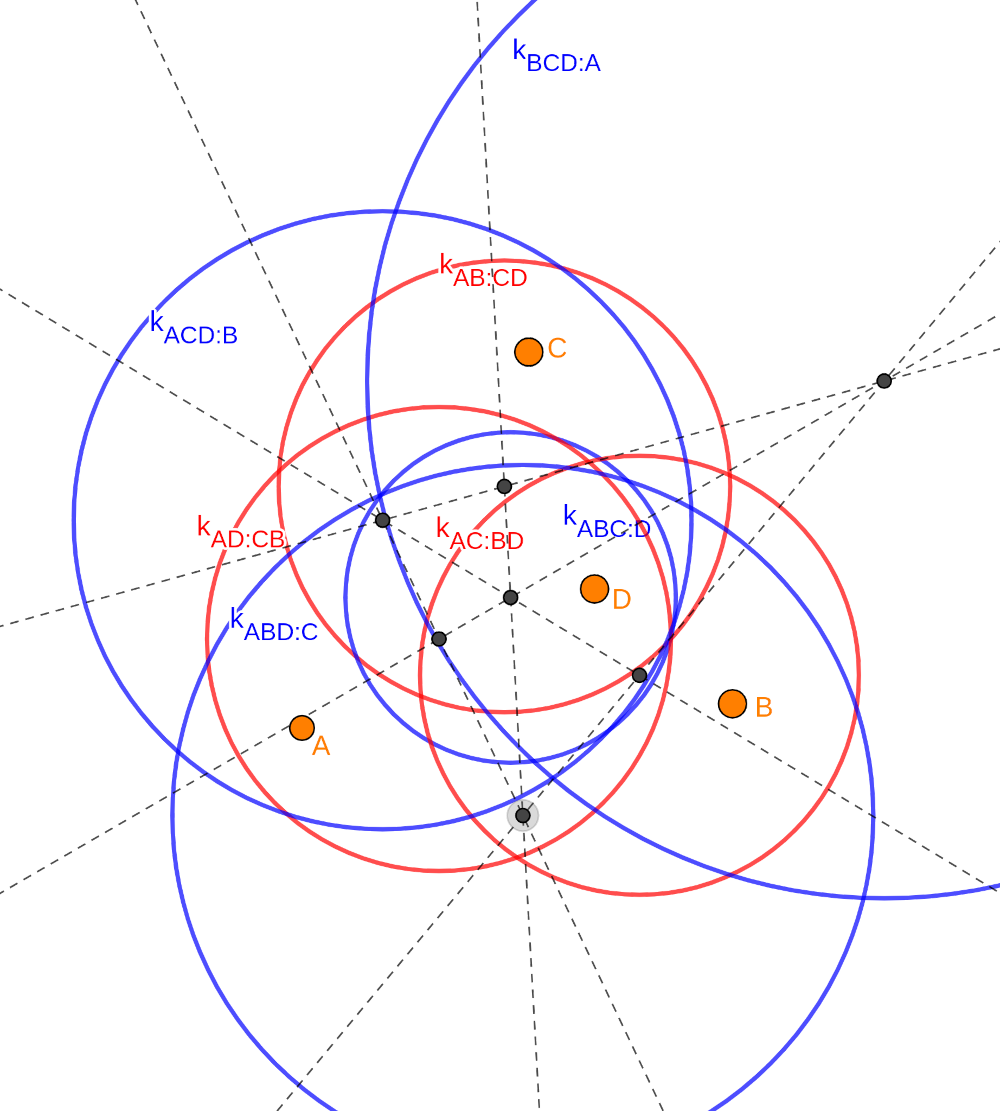
Az alábbi ábrán egy példát is mutatunk 4 pontra a 7 keresett körrel: a \(\displaystyle (2:2)\)-típusú körök pirossal, a \(\displaystyle (3:1)\)-típusú körök kékkel lettek megrajzolva, a szaggatott egyenesek a pontpárok felezőmerőlegesei.
Kiegészítés: A beadási határidő előtti napon kapott a versenybizottság egy jelzést, mely szerint elfelejtettük kikötni, hogy a négy pont nem lehet egy egyenesen. Sajnos a jelzés egy jogos hiányosságot tárt fel. Tegyük fel ugyanis, hogy \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) és \(\displaystyle D\) úgy helyezkedik el egy egyenesen, hogy \(\displaystyle AB\) és \(\displaystyle CD\) felezőmerőlegese egybeesik. Válasszuk ki ennek a felezőmerőlegesnek egy tetszőleges \(\displaystyle O\) pontját. Ha ezzel az \(\displaystyle O\) középponttal rajzolunk egy \(\displaystyle \frac{OA+OC}{2}\) sugarú kört, az egyenlő távol lesz mind a négy ponttól. Tehát az \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\) pontok ilyen elrendezése esetén Kornélia végtelen sok kört rajzolhatott volna. (A fent ismertetett megoldásban akkor vesztettük el ezt az esetet, amikor helytelenül állítottuk, hogy ha az \(\displaystyle AB\) és a \(\displaystyle CD\) szakaszok felezőmerőlegese ,,egybeesne, akkor \(\displaystyle ABCD\) szimmetrikus trapézt, azaz húrnégyszöget alkotna'' – hiszen az elfajuló szimmetrikus trapéz esetén a négy pont nem egy körön, hanem egy egyenesen van).
Mivel a feladatban úgy fogalmaztunk, hogy Kornélia megrajzolta az összes körvonalat, egyértelműen kiderült, hogy nem ezt a végtelen kört megengedő esetet szerettük volna megkerestetni a megoldókkal. Persze egy teljes diszkusszióval ellátott megoldáshoz hozzá kell tartozzon ennek az elfajuló esetnek a tisztázása is.
Mindenesetre szerencsésebb lett volna a feladat szövegében kikötnünk, hogy a négy pont nem lehet egy egyenesen sem, de sajnos ezt nem tettük meg, ezért elnézést kérünk.
Statisztika:
114 dolgozat érkezett. 5 pontot kapott: Bényei Borisz, Czanik Pál, Dang Nhat Tai, Duchon Márton, Egyházi Hanna, Farkas 512 Izabella, Foris Dávid, Jánosik Máté, Koltai Csaba Ferenc, Kovács Benedek Noel, Nguyen Kim Dorka, Sebestyén József Tas, Simon László Bence, Varga Boldizsár. 4 pontot kapott: 39 versenyző. 3 pontot kapott: 31 versenyző. 2 pontot kapott: 17 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 3 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2021. szeptemberi matematika feladatai

