 |
A B. 5186. feladat (2021. szeptember) |
B. 5186. Aladár és Béla következő játékot játssza. Rögzítenek egy \(\displaystyle n \ge 3\) számot, majd Aladár gondol egy számra az \(\displaystyle \{1,2,\ldots,n \}\) halmazból. Béla ezután tippelhet a gondolt számra. Válaszul csak azt kapja, hogy eltalálta vagy sem. Ha eltalálta, vége a játéknak.
Ha nem találta el, akkor Aladár megváltoztatja a gondolt számát úgy, hogy vagy növeli vagy csökkenti 1-gyel, de továbbra is pozitívnak kell maradnia a gondolt számnak (de \(\displaystyle n\)-nél nagyobb lehet). Béla ezután ismét tippelhet. Ezeket a lépéseket ismétlik addig, amíg Béla el nem találja az aktuálisan gondolt számot.
Bizonyítsuk be, hogy ha Béla elég ügyes, akkor a játék legkésőbb a \(\displaystyle (3n-5)\)-ödik tippjével véget ér.
Javasolta: Szoldatics József (Budapest)
(6 pont)
A beküldési határidő 2021. október 11-én LEJÁRT.
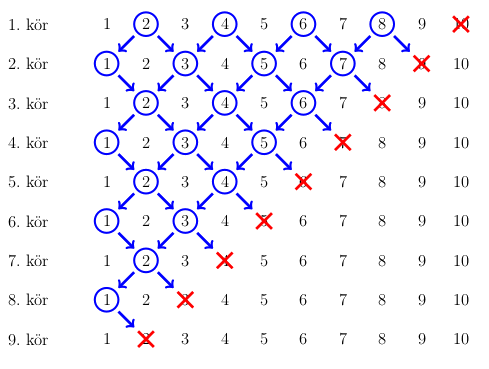
Megoldás. Legyenek Béla tippjei sorrendben a következők:
\(\displaystyle \underbrace{n-1,n-2,n-3,\ldots,3,2}_{n-2 \text{ tipp}}, \underbrace{2n-2,2n-3,2n-4,\ldots,3,2}_{2n-3 \text{ tipp}} \)
Ez összesen \(\displaystyle 3n-5\) tipp. Bebizonyítjuk, hogy valamelyik tipp biztosan eltalálja a gondolt számot.
Jelölje \(\displaystyle a_i\) az Aladár által gondolt számot Béla \(\displaystyle i\)-edik tippje előtt (azaz a kezdetben gondolt szám \(\displaystyle a_1\)).
Azt fogjuk belátni, hogy
- ha \(\displaystyle n-a_1\) páratlan, akkor az első \(\displaystyle n-2\) tipp valamelyike;
- ha pedig \(\displaystyle n-a_1\) páros, akkor az utolsó \(\displaystyle 2n-3\) tipp valamelyike talál.
Lemma. Legyen \(\displaystyle k \geq 1\) egész és tegyük fel, hogy az \(\displaystyle i\)-edik tipp előtti, Aladár által aktuálisan gondolt \(\displaystyle a_i\) szám páros és legfeljebb \(\displaystyle 2k\) (azaz a \(\displaystyle 2,4,6,\ldots,2k-2,2k\) számok valamelyike). Ekkor Béla az \(\displaystyle i\)-edik tippjével elkezdett \(\displaystyle (2k,2k-1,2k-2,\ldots,3,2)\) tippsorozattal biztosan kitalálja a gondolt számot.
Lemma bizonyítása.
Ha Béla első tippje nem talál, akkor \(\displaystyle a_i\) a \(\displaystyle 2,4,6,\ldots,2k-4,2k-2\) számok valamelyike. Ezt 1-gyel megváltoztatva
\(\displaystyle a_{i+1} \in \{ 1,3,5,\ldots,2k-3,2k-1 \}. \)
Ha \(\displaystyle a_{i+1} = 2k-1\), akkor Béla eltalálja a következő tippel, egyébként Aladár 1-gyel változtat, így
\(\displaystyle a_{i+2} \in \{ 2,4,6,\ldots,2k-4,2k-2 \}. \)
Ha \(\displaystyle a_{i+2} = 2k-2\), akkor Béla talál a következő tippel, egyébként Aladár 1-gyel változtat, így
\(\displaystyle a_{i+3} \in \{ 1,3,5,\ldots,2k-5,2k-3 \}. \)
Ezt folytatva látható, hogy ha Béla addig nem talált, és \(\displaystyle j\) páros, akkor
\(\displaystyle a_{i+j} \in \{ 2,4,6,\ldots,2k-4,2k-j \}, \)
míg ha \(\displaystyle j\) páratlan, akkor
\(\displaystyle a_{i+j} \in \{ 1,3,5,\ldots,2k-4,2k-j \}. \)
Így \(\displaystyle j=2k-2\) esetén \(\displaystyle a_{i+2k-2}\) már csak 2 lehet, így (legkésőbb) az \(\displaystyle (i+2k-2)\)-edik tippel Béla biztosan talál. (Lemma bizonyításának vége.)
A megoldást az \(\displaystyle n\) és az \(\displaystyle a_1\) paritása szerinti esetszétválasztással fejezzük be.
- Ha \(\displaystyle n\) páratlan, de \(\displaystyle a_1\) páros, akkor \(\displaystyle i=1\) és \(\displaystyle 2k = n\) választással alkalmazhatjuk a lemmát, tehát az első \(\displaystyle n-2\) tipp valamelyike talál.
- Ha \(\displaystyle n\) páros, de \(\displaystyle a_1\) páratlan, akkor vagy talál az első, \(\displaystyle (n-1)\)-es tipp , vagy \(\displaystyle a_2 \in \{2,4,\ldots,n-2\}\) páros szám, azaz most \(\displaystyle i=2\) és \(\displaystyle 2k = n-2\) választással tudjuk alkalmazni a lemmát. Ezzel megint beláttuk, hogy az első \(\displaystyle n-2\) tipp valamelyike talál.
- Ha \(\displaystyle n\) és \(\displaystyle a_1\) ugyanolyan paritású, akkor az első \(\displaystyle n-2\) tipp egyike sem találhat, hiszen Béla tippje mindig az aktuálisan gondolt számmal ellentétes paritású. Az \(\displaystyle n-2\) sikertelen tipp után így
\(\displaystyle a_{n-1} \in \{ 2,4,6,\ldots,2n-4,2n-2 \}, \)
hiszen egyrészt \(\displaystyle a_{n-1} \leq a_1 + n-2 \leq n + (n-2)\), másrészt mivel \(\displaystyle (n-2)\)-szer változott meg \(\displaystyle a_1\)-hez képest a paritása, ezért \(\displaystyle a_{n-1}\) biztosan páros. A lemma \(\displaystyle i=n-1\) és \(\displaystyle 2k=2n-2\) választással befejezi a megoldásunkat.
Statisztika:
A KöMaL 2021. szeptemberi matematika feladatai

