 Problem B. 5186. (September 2021)
Problem B. 5186. (September 2021)
B. 5186. Al and Bill are playing the following game. They agree on a fixed number \(\displaystyle n \ge 3\), and then Al thinks of a number from the set \(\displaystyle \{1,2,\ldots,n \}\). Now Bill can guess the number. He will only get yes or no answers. If the answer is yes, the game terminates.
If the answer is no, Al will change the number: either increases or reduces it by 1, but the number must remain positive (it is allowed to go beyond \(\displaystyle n\) though). Then Bill can guess again, trying to hit the new number. The procedure is repeated until finally Bill gets the number.
Prove that Bill has a strategy to end the game with at most \(\displaystyle (3n-5)\) guesses.
Proposed by J. Szoldatics, Budapest
(6 pont)
Deadline expired on October 11, 2021.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Legyenek Béla tippjei sorrendben a következők:
\(\displaystyle \underbrace{n-1,n-2,n-3,\ldots,3,2}_{n-2 \text{ tipp}}, \underbrace{2n-2,2n-3,2n-4,\ldots,3,2}_{2n-3 \text{ tipp}} \)
Ez összesen \(\displaystyle 3n-5\) tipp. Bebizonyítjuk, hogy valamelyik tipp biztosan eltalálja a gondolt számot.
Jelölje \(\displaystyle a_i\) az Aladár által gondolt számot Béla \(\displaystyle i\)-edik tippje előtt (azaz a kezdetben gondolt szám \(\displaystyle a_1\)).
Azt fogjuk belátni, hogy
- ha \(\displaystyle n-a_1\) páratlan, akkor az első \(\displaystyle n-2\) tipp valamelyike;
- ha pedig \(\displaystyle n-a_1\) páros, akkor az utolsó \(\displaystyle 2n-3\) tipp valamelyike talál.
Lemma. Legyen \(\displaystyle k \geq 1\) egész és tegyük fel, hogy az \(\displaystyle i\)-edik tipp előtti, Aladár által aktuálisan gondolt \(\displaystyle a_i\) szám páros és legfeljebb \(\displaystyle 2k\) (azaz a \(\displaystyle 2,4,6,\ldots,2k-2,2k\) számok valamelyike). Ekkor Béla az \(\displaystyle i\)-edik tippjével elkezdett \(\displaystyle (2k,2k-1,2k-2,\ldots,3,2)\) tippsorozattal biztosan kitalálja a gondolt számot.
Lemma bizonyítása.
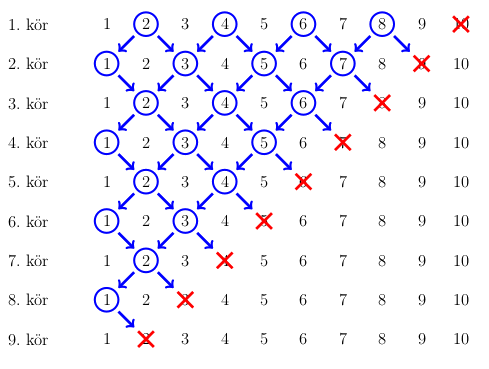
Ha Béla első tippje nem talál, akkor \(\displaystyle a_i\) a \(\displaystyle 2,4,6,\ldots,2k-4,2k-2\) számok valamelyike. Ezt 1-gyel megváltoztatva
\(\displaystyle a_{i+1} \in \{ 1,3,5,\ldots,2k-3,2k-1 \}. \)
Ha \(\displaystyle a_{i+1} = 2k-1\), akkor Béla eltalálja a következő tippel, egyébként Aladár 1-gyel változtat, így
\(\displaystyle a_{i+2} \in \{ 2,4,6,\ldots,2k-4,2k-2 \}. \)
Ha \(\displaystyle a_{i+2} = 2k-2\), akkor Béla talál a következő tippel, egyébként Aladár 1-gyel változtat, így
\(\displaystyle a_{i+3} \in \{ 1,3,5,\ldots,2k-5,2k-3 \}. \)
Ezt folytatva látható, hogy ha Béla addig nem talált, és \(\displaystyle j\) páros, akkor
\(\displaystyle a_{i+j} \in \{ 2,4,6,\ldots,2k-4,2k-j \}, \)
míg ha \(\displaystyle j\) páratlan, akkor
\(\displaystyle a_{i+j} \in \{ 1,3,5,\ldots,2k-4,2k-j \}. \)
Így \(\displaystyle j=2k-2\) esetén \(\displaystyle a_{i+2k-2}\) már csak 2 lehet, így (legkésőbb) az \(\displaystyle (i+2k-2)\)-edik tippel Béla biztosan talál. (Lemma bizonyításának vége.)
A megoldást az \(\displaystyle n\) és az \(\displaystyle a_1\) paritása szerinti esetszétválasztással fejezzük be.
- Ha \(\displaystyle n\) páratlan, de \(\displaystyle a_1\) páros, akkor \(\displaystyle i=1\) és \(\displaystyle 2k = n\) választással alkalmazhatjuk a lemmát, tehát az első \(\displaystyle n-2\) tipp valamelyike talál.
- Ha \(\displaystyle n\) páros, de \(\displaystyle a_1\) páratlan, akkor vagy talál az első, \(\displaystyle (n-1)\)-es tipp , vagy \(\displaystyle a_2 \in \{2,4,\ldots,n-2\}\) páros szám, azaz most \(\displaystyle i=2\) és \(\displaystyle 2k = n-2\) választással tudjuk alkalmazni a lemmát. Ezzel megint beláttuk, hogy az első \(\displaystyle n-2\) tipp valamelyike talál.
- Ha \(\displaystyle n\) és \(\displaystyle a_1\) ugyanolyan paritású, akkor az első \(\displaystyle n-2\) tipp egyike sem találhat, hiszen Béla tippje mindig az aktuálisan gondolt számmal ellentétes paritású. Az \(\displaystyle n-2\) sikertelen tipp után így
\(\displaystyle a_{n-1} \in \{ 2,4,6,\ldots,2n-4,2n-2 \}, \)
hiszen egyrészt \(\displaystyle a_{n-1} \leq a_1 + n-2 \leq n + (n-2)\), másrészt mivel \(\displaystyle (n-2)\)-szer változott meg \(\displaystyle a_1\)-hez képest a paritása, ezért \(\displaystyle a_{n-1}\) biztosan páros. A lemma \(\displaystyle i=n-1\) és \(\displaystyle 2k=2n-2\) választással befejezi a megoldásunkat.
Statistics:
Problems in Mathematics of KöMaL, September 2021
