Problem B. 5189. (September 2021)

B. 5189. The base edge of a right pyramid with a regular triangular base is \(\displaystyle a\). Let \(\displaystyle r\) be the radius of the inscribed sphere, and let \(\displaystyle R\) be the radius of the escribed sphere touching the base. Prove that \(\displaystyle a^2=12rR\).

Proposed by L. László, Budapest

(6 pont)

Deadline expired on October 11, 2021.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen a gúla alaplapja \(\displaystyle ABC\), a negyedik csúcsa \(\displaystyle D\), a \(\displaystyle BC\) él felezőpontja \(\displaystyle F\), a beírt gömb középpontja \(\displaystyle I\), az alaplaphoz hozzáírt gömb középpontja \(\displaystyle J\), a gömbök közös érintési pontja, egyben az alaplap középpontja \(\displaystyle T\), végül a két gömb érintési pontjai a \(\displaystyle BCD\) síkon \(\displaystyle U\), illetve \(\displaystyle V\). Az ábra szimmetrikus az \(\displaystyle ADF\) síkra, amely egyben a \(\displaystyle BC\) szakasz felező merőleges síkja is, ezért az \(\displaystyle I\), \(\displaystyle J\), \(\displaystyle U\) és \(\displaystyle V\) pontok is ebben a síkban vannak. A sík a két gömböt egy-egy főkörük mentén metszi; ezek a \(\displaystyle DF\) félegyenesnek azonos, az \(\displaystyle AF\) szakasznak ellentétes oldalán fekszenek az \(\displaystyle ADF\) síkban. A két körnek a \(\displaystyle DF\) egyenes az egyik külső, az \(\displaystyle AF\) szakasz pedig az egyik belső közös érintője.

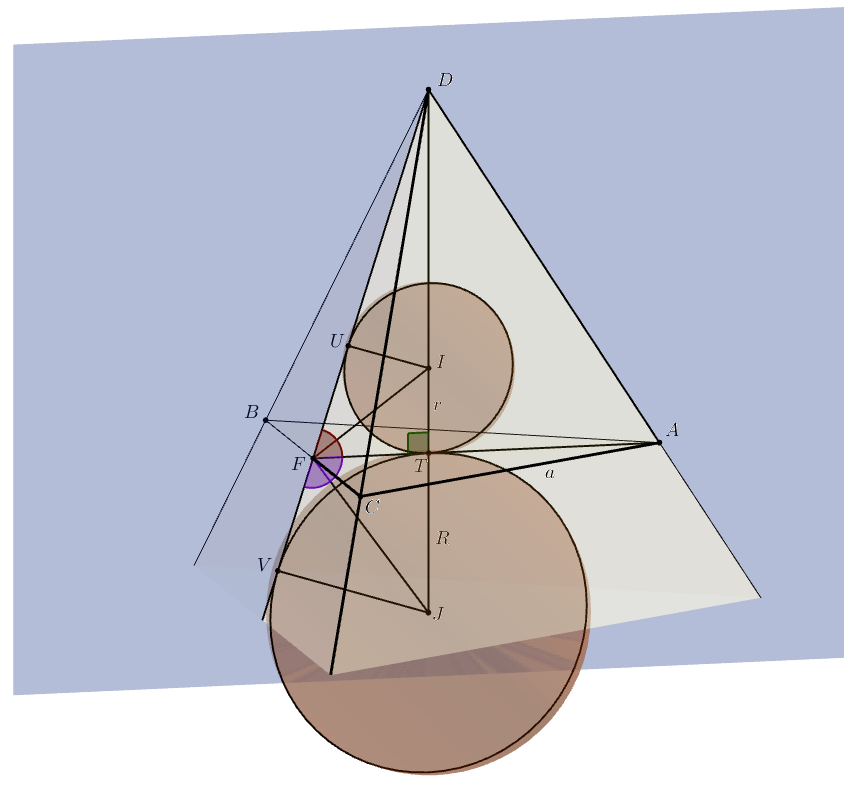
Az \(\displaystyle FI\) és az \(\displaystyle FJ\) szakasz felezi a \(\displaystyle TFU\), illetve a \(\displaystyle TFV\) szöget, ezért \(\displaystyle IFJ\sphericalangle=90^\circ\); az \(\displaystyle FIJ\) egy derékszögű háromszög, amelynek átfogóhoz tartozó magassága az \(\displaystyle FT\) szakasz. Az átfogó két darabja \(\displaystyle TI=r\), illetve \(\displaystyle TJ=R\). Az \(\displaystyle a\) oldalú, szabályos \(\displaystyle ABC\) háromszög magassága \(\displaystyle AF=\frac{\sqrt3}2a\), ezt a \(\displaystyle T\) közép-, egyben súlypont harmadolja, tehát \(\displaystyle FT=\frac13AF=\frac{a}{2\sqrt3}\).

Ezek után írjuk fel a magasságtételt az \(\displaystyle FIJ\) háromszögben:

\(\displaystyle FT^2 = TI\cdot TJ,\)

\(\displaystyle \left(\frac{a}{2\sqrt3}\right)^2 = rR; \)

átrendezve

\(\displaystyle a^2=12rR. \)

Statistics:

79 students sent a solution.
6 points:	Andai Márk, Baski Bence, Bényei Borisz, Bognár 171 András Károly, Christ Miranda Anna, Csonka Illés, Duchon Márton, Fekete Richárd, Gömze Norken, Horváth 530 Mihály, Horváth Hanna Szabrina, Jánosik Máté, Juhász-Molnár Erik, Kalocsai Zoltán, Kercsó-Molnár Anita, Koleszár Domonkos, Kun Ágoston , Laskai Botond, László Anna, Lőw László, Makrai-Kis Balázs, Nádor Artúr, Nádor Benedek, Nagy 551 Levente, Romaniuc Albert-Iulian, Sándor Péter, Sebestyén József Tas, Simon László Bence, Somogyi Dalma, Tarján Bernát, Tekes János, Tusnády Sámuel, Varga Boldizsár, Wiener Anna, Zömbik Barnabás.
5 points:	19 students.
4 points:	9 students.
3 points:	3 students.
2 points:	3 students.
1 point:	4 students.
0 point:	1 student.
Unfair, not evaluated:	3 solutionss.

Problems in Mathematics of KöMaL, September 2021