Problem B. 5193. (October 2021)

B. 5193. In an acute-angled triangle \(\displaystyle ABC\), \(\displaystyle \angle BCA =45^{\circ}\), the feet of the altitudes on sides \(\displaystyle BC\), \(\displaystyle CA\), \(\displaystyle AB\) are \(\displaystyle D\), \(\displaystyle E\), \(\displaystyle F\), respectively, and the orthocentre is \(\displaystyle M\). Point \(\displaystyle F\) divides line segment \(\displaystyle AB\) in a ratio \(\displaystyle {AF}:{FB}={2}:{3}\). \(\displaystyle G\) is the point on side \(\displaystyle AC\) for which \(\displaystyle CG=BM\). Show that the centroid of triangle \(\displaystyle ABG\) is \(\displaystyle M\).

(4 pont)

Deadline expired on November 10, 2021.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás.

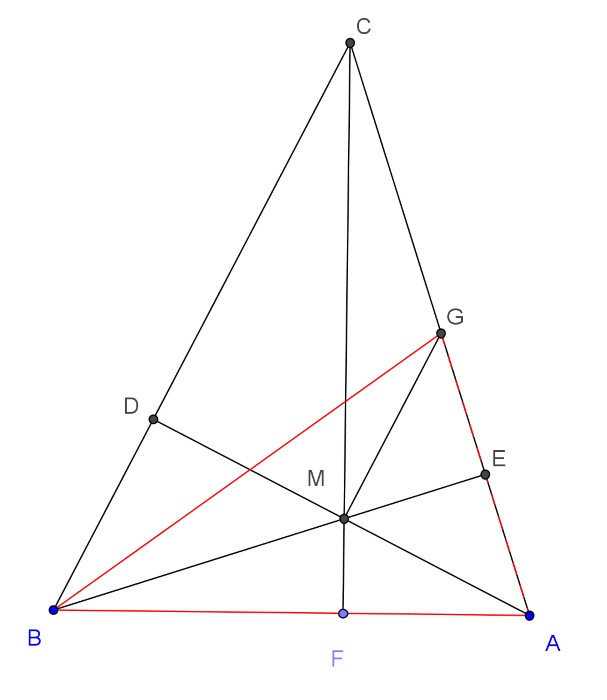
Az \(\displaystyle ABC\) háromszög \(\displaystyle C\)-nél fekvő szöge \(\displaystyle 45^{\circ}\), a \(\displaystyle D\) és \(\displaystyle E\) pontok magasságok talppontjai, így \(\displaystyle CBE\sphericalangle=DAC\sphericalangle=45^{\circ}\). A \(\displaystyle BMGC\) négyszög \(\displaystyle BC\) oldalon fekvő szögei \(\displaystyle 45^{\circ}\)-osak, továbbá \(\displaystyle BM=CG\), tehát a négyszög szimmetrikus trapéz. A trapéz \(\displaystyle G\)-nél fekvő külső szöge, az \(\displaystyle AGM\sphericalangle=45^{\circ}\). Ezzel beláttuk, hogy \(\displaystyle AGM\) egyenlő szárú háromszög, azaz \(\displaystyle BE\) súlyvonala az \(\displaystyle ABG\) egyenlő szárú háromszögnek. A bizonyítás befejezéséhez elegendő megmutatni, hogy az \(\displaystyle M\) pont harmadolja az \(\displaystyle EB\) szakaszt.

A szögek alapján \(\displaystyle EM=AE\). Az \(\displaystyle EMC\) és \(\displaystyle EAB\) derékszögű háromszögekben egy-egy befogó és a velük szemközti szög is egyforma, a két háromszög egybevágó, vagyis \(\displaystyle MC=AB\). Szintén a szögek alapján az is igaz, hogy \(\displaystyle AEB\bigtriangleup \sim AFC\bigtriangleup\). Írjuk fel az eddigi megállapítások felhasználásával az \(\displaystyle EM\) és \(\displaystyle EB\) szakaszok \(\displaystyle x\) arányát:

\(\displaystyle x=\frac{EM}{EB}=\frac{AE}{EB}=\frac{AF}{FC}=\frac{AF}{AB+MF}.\)

Az \(\displaystyle AEB\) és \(\displaystyle MFB\) derészögű háromszögek hasonlósága alapján pedig:

\(\displaystyle x=\frac{EM}{EB}=\frac{EA}{EB}=\frac{MF}{FB}\)

is teljesül. Ezzel kiegészítve a fentebbi gondolatmenetet:

\(\displaystyle x=\frac{AF}{AB+MF}=\frac{AF}{AB+xBF}=\frac{\frac{2}{2}AB}{AB+x\cdot \frac{3}{5}AB}.\)

Most az \(\displaystyle AB\)-vel egyszerűsítve rendezés után \(\displaystyle x\)-re másodfokú egyenletet kapunk:

\(\displaystyle x=\frac{2}{5+3x}, \)

\(\displaystyle 3x^2+5x-2=0.\)

Az egyenlet pozitív gyöke \(\displaystyle x=\frac{1}{3}\).

Beláttuk, hogy az \(\displaystyle M\) pont az \(\displaystyle ABG\) egyenlő szárú háromszög alaphoz tartozó magasságának harmadolópontja, tehát valóban a súlypont.

Statistics:

97 students sent a solution.
4 points:	57 students.
3 points:	16 students.
2 points:	13 students.
1 point:	7 students.
0 point:	2 students.

Problems in Mathematics of KöMaL, October 2021