Problem B. 5194. (October 2021)

B. 5194. In a triangle \(\displaystyle ABC\), \(\displaystyle \angle ABC =2\angle CAB\). Side \(\displaystyle AB\) touches the inscribed circle at point \(\displaystyle E\), and intersects the angle bisector drawn from \(\displaystyle C\) at point \(\displaystyle F\). Prove that \(\displaystyle AF=2BE\).

(4 pont)

Deadline expired on November 10, 2021.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyenek az \(\displaystyle ABC\) háromszög szögei a szokásos módon \(\displaystyle \alpha\), \(\displaystyle \beta\) és \(\displaystyle \gamma\); a feltétel szerint \(\displaystyle \beta=2\alpha\). Legyen az \(\displaystyle AB\) oldalhoz hozzáírt kör középontja \(\displaystyle J\), és a hozzáírt kör érintési pontja az \(\displaystyle AB\) oldalon \(\displaystyle E_1\). Jól ismert, hogy \(\displaystyle AE_1=BE=s-b\), ahol \(\displaystyle b=AC\) és \(\displaystyle s\) az \(\displaystyle ABC\) háromszög félkerülete.

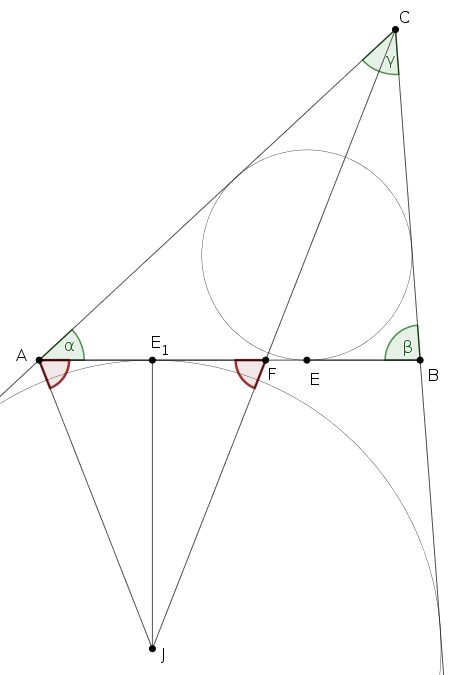
Az \(\displaystyle A\)-nál levő szögek összeszámolásából

\(\displaystyle JAF\angle = \dfrac{180^\circ-BAC\angle}{2} = 90^\circ-\dfrac\alpha2, \)

az \(\displaystyle AFC\) háromszög szögeiből

\(\displaystyle AFJ\angle = FAC\angle+ACF\angle = \alpha+\dfrac\gamma2 = \dfrac\beta2+\bigg(90^\circ-\dfrac\alpha2-\dfrac\beta2\bigg) = 90^\circ-\dfrac\alpha2 = JAF\angle. \)

Tehát \(\displaystyle AFJ\angle=JFA\); a \(\displaystyle JFA\) háromszög egyenlő szárú, ezért

\(\displaystyle AF = 2AE_1 = 2BE. \)

Statistics:

80 students sent a solution.
4 points:	65 students.
3 points:	7 students.
2 points:	1 student.
1 point:	4 students.
Unfair, not evaluated:	1 solutions.

Problems in Mathematics of KöMaL, October 2021