Problem B. 5200. (November 2021)

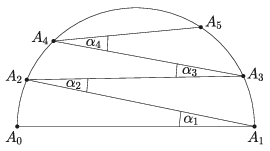
B. 5200. The diameter of a semicircular arc is \(\displaystyle A_0A_1=1\). A point \(\displaystyle A_2\) is selected on the arc, such that \(\displaystyle \angle A_0A_1A_2 =1^\circ\). Then a point \(\displaystyle A_3\) is selected on the arc \(\displaystyle A_1A_2\), such that \(\displaystyle \angle A_1A_2A_3 =2^\circ\). The procedure is continued: point \(\displaystyle A_{k+1}\) is selected on the arc \(\displaystyle A_{k-1}A_k\), so that the measure of angle \(\displaystyle A_{k-1}A_kA_{k+1}\) is \(\displaystyle k\) degrees (\(\displaystyle k=3,4,\ldots,9\)). What will be the length of the line segment \(\displaystyle A_9A_{10}\)? (The figure is not to scale.)

(3 pont)

Deadline expired on December 10, 2021.

Sorry, the solution is available only in Hungarian. Google translation

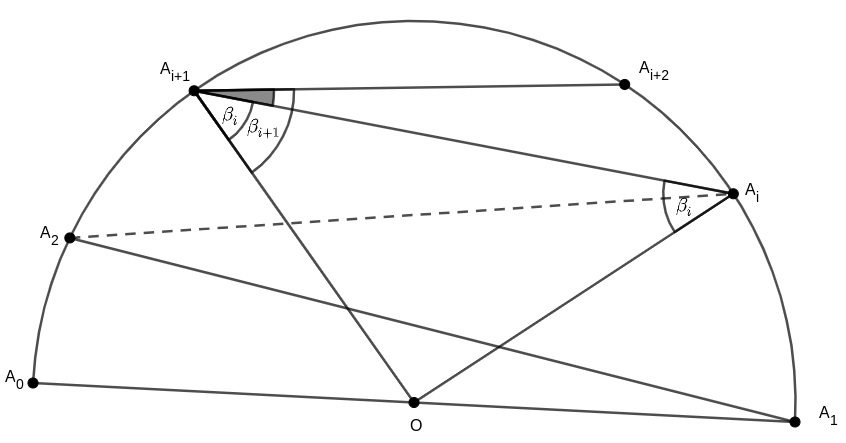
Megoldás. Kössük össze az \(\displaystyle A_i\) pontokat a félkörvonal \(\displaystyle O\) középpontjával, és vezessük be az \(\displaystyle OA_iA_{i+1}\angle=\beta_i\) jelölést. Világos, hogy \(\displaystyle \beta_1=1^\circ\). Továbbá mivel az \(\displaystyle OA_iA_{i+1}\triangle\) egyenlő szárú, így

\(\displaystyle \beta_{i+1}=OA_{i+1}A_{i+2}\angle=OA_{i+1}A_{i}\angle+A_iA_{i+1}A_{i+2}\angle=\beta_i+(i+1)^\circ\qquad (i=1,2,\ldots,8).\)

Ezt nyolcszor alkalmazva \(\displaystyle \beta_9=45^\circ\), tehát \(\displaystyle OA_9A_{10}\) derékszögű egyenlő szárú háromszög. Végül Pitagorasz-tétellel \(\displaystyle A_9A_{10}=\sqrt{(1/2)^2+(1/2)^2}=\sqrt 2/2\) adódik.

Statistics:

108 students sent a solution.
3 points:	76 students.
2 points:	21 students.
1 point:	2 students.
0 point:	2 students.
Unfair, not evaluated:	5 solutionss.

Problems in Mathematics of KöMaL, November 2021