Problem B. 5203. (November 2021)

B. 5203. In a triangle \(\displaystyle ABC\), \(\displaystyle AB>BC\), the inscribed circle touches sides \(\displaystyle BC\), \(\displaystyle CA\) and \(\displaystyle AB\) at the points \(\displaystyle A_0\), \(\displaystyle B_0\) és \(\displaystyle C_0\), respectively, and the escribed circle drawn to side \(\displaystyle AC\) touches \(\displaystyle AC\) at point \(\displaystyle B_1\). Show that the intersection of the line segments \(\displaystyle A_0B_1\) and \(\displaystyle B_0C_0\) lies on the interior angle bisector drawn from vertex \(\displaystyle B\) if and only if the angle at vertex \(\displaystyle C\) measures \(\displaystyle 90^{\circ}\).

Proposed by G. Holló, Budapest

(5 pont)

Deadline expired on December 10, 2021.

Sorry, the solution is available only in Hungarian. Google translation

1. megoldás(vázlat). Legyen a beírt kör középpontja \(\displaystyle O\), a \(\displaystyle C\) pont merőleges vetülete a \(\displaystyle BO\) és \(\displaystyle AO\) szögfelezőkön \(\displaystyle P\), illetve \(\displaystyle Q\). A Thalész-tétel megfordítása miatt a \(\displaystyle C\), \(\displaystyle O\), \(\displaystyle A_0\), \(\displaystyle B_0\), \(\displaystyle P\), \(\displaystyle Q\) pontok egy körön vannak, legyen ez \(\displaystyle k\). Jól ismert, hogy \(\displaystyle CB_0=AB_1\). A háromszög félszögei legyenek \(\displaystyle \alpha,\beta,\gamma\), ezek összege \(\displaystyle 90^\circ\).

Vegyük észre, hogy \(\displaystyle AB_0C_0\sphericalangle=90^\circ-\alpha=\beta+\gamma\), másrészt a \(\displaystyle k\) körből és a \(\displaystyle BCO\) háromszögből \(\displaystyle AB_0P\sphericalangle=COP\sphericalangle=\beta+\gamma\), ezért a \(\displaystyle B_0C_0\) egyenes átmegy \(\displaystyle P\)-n. A \(\displaystyle P\) tehát a \(\displaystyle BO\) szögfelező és a \(\displaystyle B_0C_0\) egyenes meszéspontja, és az a kérdés, hogy az \(\displaystyle A_0B_1\) egyenes is átmegy-e a \(\displaystyle P\) ponton.

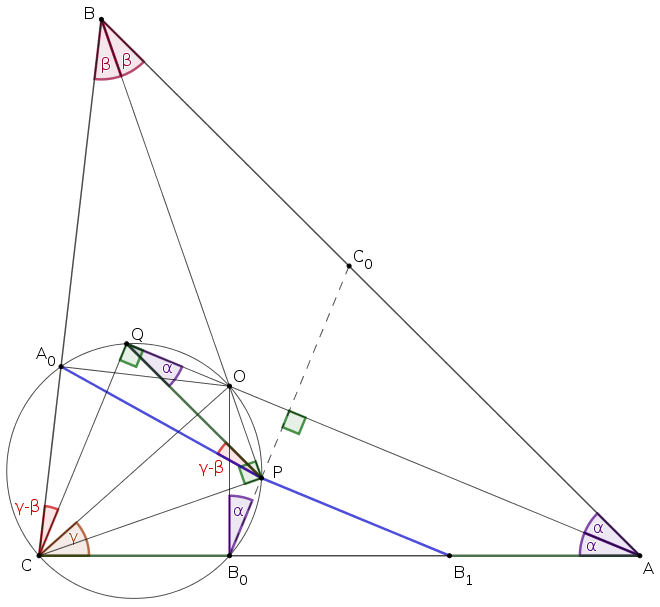
\(\displaystyle CQ\) és \(\displaystyle B_0P\) párhuzamosak, mert mindkettő merőleges az \(\displaystyle AO\) szögfelezőre, így \(\displaystyle QCB_0P\) húrtrapéz, amiből \(\displaystyle QP=CB_0=AB_1\). Továbbá, az \(\displaystyle AOB_0\) derékszögű háromszögben \(\displaystyle AQP\sphericalangle=OB_0P\sphericalangle=B_1AQ\sphericalangle=\alpha\); ebből következik, hogy \(\displaystyle AQPB_1\) szimmetrikus trapéz és \(\displaystyle AQ\parallel B_1P\).

Ezen kívül kiszámítjuk az \(\displaystyle A_0PQ\sphericalangle\) szöget is: a \(\displaystyle CAQ\) háromszögből \(\displaystyle A_0PQ\sphericalangle=A_0CQ\sphericalangle=BCA\sphericalangle-QCA\sphericalangle=2\gamma-(90^\circ-\alpha)=\gamma-\beta\).

Ezek után az \(\displaystyle A_0B_1\) egyenes akkor és csak akkor megy át a \(\displaystyle P\) ponton, ha \(\displaystyle A_0P\parallel AQ\), avagy \(\displaystyle A_0PQ\sphericalangle=AQP\sphericalangle\), vagyis \(\displaystyle \gamma-\beta=\alpha\), azaz \(\displaystyle \gamma=45^\circ\), tehát \(\displaystyle BCA\sphericalangle=90^\circ\).

2. megoldás. Az oldalakat és a szögeket a szokásos módon betűzzük, \(\displaystyle O\) jelöli a beírt kör középpontját, továbbá legyen \(\displaystyle s\) a háromszög félkerülete: \(\displaystyle 2s=a+b+c\); az \(\displaystyle A_0B_1\) és \(\displaystyle B_0C_0\) szakaszok metszéspontja pedig \(\displaystyle M\). Ismert, hogy a beírt- és hozzáírt körökhöz a csúcsokból húzott érintőszakaszok hosszai az oldalakkal kifejezhetők: \(\displaystyle AB_0=AC_0=x=s-a\), \(\displaystyle BA_0=BC_0=y=s-b\) és \(\displaystyle CA_0=CB_0=z=s-c\); valamint \(\displaystyle AB_1=z=s-c\).

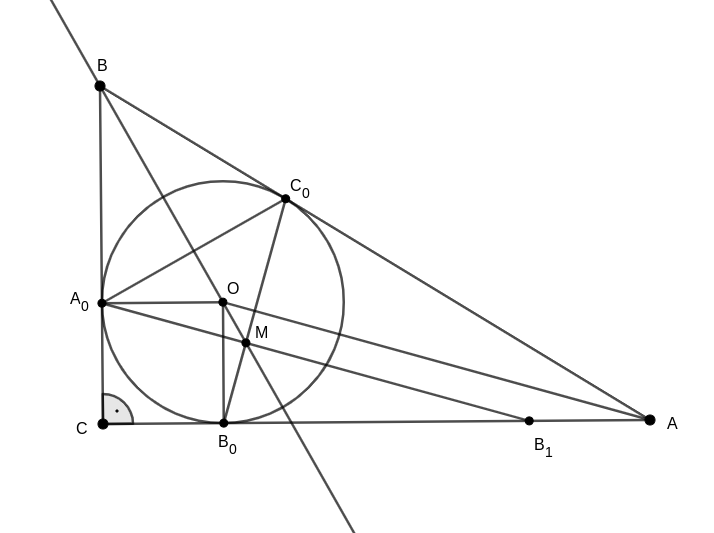
Először tegyük fel, hogy az \(\displaystyle ABC\) háromszög derékszögű, \(\displaystyle C\angle= 90^\circ\). Ekkor a \(\displaystyle CA_0OB_0\) négyszög egyszerre téglalap és deltoid, ezért négyzet. \(\displaystyle CB_0\) párhuzamos és egyenlő hosszú \(\displaystyle A_0O\)-val és \(\displaystyle B_1A\)-val is, emiatt a \(\displaystyle B_1AOA_0\) négyszög paralelogramma. A \(\displaystyle B_0AC_0\) egyenlő szárú háromszögben a szárszög \(\displaystyle AO\) szögfelezője merőleges a \(\displaystyle B_0C_0\) alapra, így a vele párhuzamos \(\displaystyle A_0B_1\) egyenes is: \(\displaystyle A_0B_1\perp B_0C_0\).

Tudjuk továbbá, hogy \(\displaystyle A_0C_0B_0\angle=180^\circ-A_0C_0B\angle-B_0C_0A\angle=180^\circ-(90^\circ - \beta/2)-(90^\circ -\alpha/2)=(\alpha+\beta)/2=45^\circ.\) Ebből következik, hogy az \(\displaystyle A_0MC_0\) háromszög derékszögű, egyenlő szárú háromszög, azaz \(\displaystyle M\) illeszkedik \(\displaystyle A_0C_0\) szakaszfelező merőlegesére, ami pedig \(\displaystyle BA_0=BC_0\) miatt épp a \(\displaystyle B\)-hez tartozó belső szögfelező. Ezzel az állítás ,,akkor" részét megmutattuk.

Most tegyük fel, hogy \(\displaystyle M\) illeszkedik a \(\displaystyle B\)-ből induló belső szögfelezőre. Először szögszámolással igazoljuk, hogy \(\displaystyle A_0CB_1\triangle \sim B_0MB_1\triangle\). Az \(\displaystyle AC_0B_0\) egyenlő szárú háromszögben \(\displaystyle C_0B_0A\angle=B_0C_0A\angle=90^\circ-\alpha/2\), továbbá ebből adódóan \(\displaystyle B_0C_0B\angle=90^\circ +\alpha/2\). Ahogy korábban, \(\displaystyle A_0\) és \(\displaystyle C_0\) pontok szimmetrikusak a \(\displaystyle B\)-nél lévő szög \(\displaystyle BM\) belső szögfelezőjére, emiatt \(\displaystyle MA_0B\angle=MC_0B\angle=90^\circ +\alpha/2\), s így \(\displaystyle CA_0B_1\angle=90^\circ-\alpha/2\). Ezekből \(\displaystyle MB_0B_1\angle=CA_0B_1\angle\), s mivel \(\displaystyle B_1\)-nél levő szögük közös, így valóban \(\displaystyle A_0CB_1\triangle \sim B_0MB_1\triangle\). Ebből következően a megfelelő oldalak aránya egyenlő:

\(\displaystyle \frac{MB_0}{MB_1}=\frac{CA_0}{CB_1}=\frac{s-c}{b-(s-c)}=\frac{s-c}{s-a}.\)

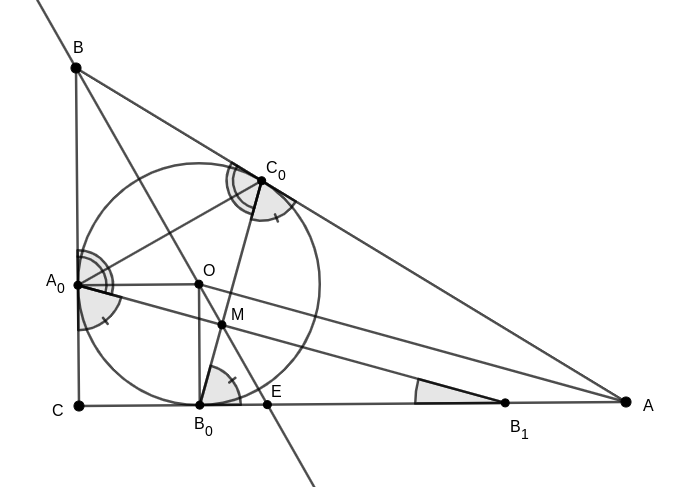
Messe \(\displaystyle BM\) az \(\displaystyle AC\) oldalt \(\displaystyle E\)-ben. Világos, hogy \(\displaystyle BM\) felezi \(\displaystyle B_1MB_0\angle\)-t is. Felírhatjuk a szögfelező-tételt \(\displaystyle ABC\) és \(\displaystyle B_1MB_0\) háromszögekre, amiből

\(\displaystyle \frac{CE}{EA}=\frac{a}{c} \quad \text{és} \quad \frac{B_0E}{EB_1}=\frac{B_0M}{MB_1}=\frac{s-c}{s-a}.\)

Felhasználva hogy \(\displaystyle B_0B_1=b-CB_0-B_1A=b-2(s-c)=c-a\), arányos osztással kifejezhető \(\displaystyle CE\) és \(\displaystyle B_0E\) szakaszok hossza is:

\(\displaystyle CE=\frac{a}{a+c}\cdot b \quad \text{és} \quad B_0E=\frac{s-c}{(s-c)+(s-a)}\cdot (c-a)=\frac{(s-c)(c-a)}{b}.\)

Végül \(\displaystyle CE=CB_0+B_0E\), azaz

\(\displaystyle \frac{ab}{a+c}=(s-c)+\frac{(s-c)(c-a)}{b},\)

a jobb oldalon \(\displaystyle (s-c)\)-t kiemelve, és alakítva

\(\displaystyle \frac{ab}{a+c}=\frac{b^2-(a-c)^2}{2b}.\)

Ebből keresztbeszorzás és rendezés után \(\displaystyle ab^2-cb^2=-a(a-c)^2-c(a-c)^2\), amit \(\displaystyle (a-c)\)-vel elosztva, majd ismét rendezve \(\displaystyle a^2+b^2=c^2\) adódik. Így a Pitagorasz-tétel megfordításából következik, hogy \(\displaystyle C\)-nél valóban derékszög van, és ezzel a bizonyítás teljes.

3. megoldás(vázlat). (Csúnya, de célratörő.) Legyen \(\displaystyle X=AB\cap A_0B_1\), \(\displaystyle Y=BC\cap B_0C_0\), \(\displaystyle x=BX\) és \(\displaystyle y=BY\). Ezeket előjelesen számoljuk, a \(\displaystyle BA\) és \(\displaystyle BC\) félegyenesek iránya a pozitív.

Mivel \(\displaystyle BA_0=BC_0\), a \(\displaystyle B_0C_0\) és \(\displaystyle A_0B_1\) egyenesek akkor és csak akkor metszik egymást a szögfelezőn, ha \(\displaystyle X\) és \(\displaystyle Y\) egymás tükörképe a szögfelezőre, vagyis \(\displaystyle x=y\).

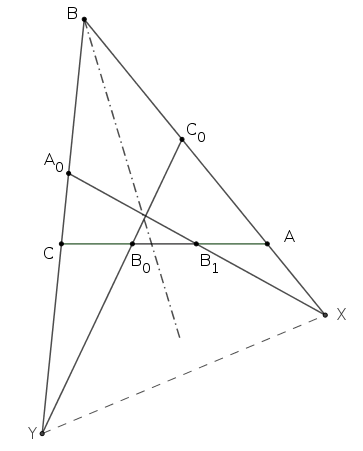
Alkalmazzuk Menelaosz tételét az \(\displaystyle ABC\) háromszögre és az \(\displaystyle A_0B_1X\) egyenesre:

\(\displaystyle \dfrac{AX}{XB}\cdot\dfrac{BA_0}{A_0C}\cdot\dfrac{CB_1}{B_1A} = \dfrac{c-x}{x}\cdot\dfrac{s-b}{s-c}\cdot\frac{s-a}{s-c} = -1, \qquad x = \frac{c(s-a)(s-b)}{(s-a)(s-b)-(s-c)^2}. \)

Most pedig tekintsük a Menelaosz-tételt az \(\displaystyle ABC\) háromszögre és a \(\displaystyle C_0B_0Y\) egyenesre:

\(\displaystyle \dfrac{BY}{YC}\cdot\dfrac{CB_0}{B_0A}\cdot\dfrac{AC_0}{C_0B} = \dfrac{y}{a-y}\cdot\dfrac{s-c}{s-a}\cdot\frac{s-a}{s-b} = -1, \qquad y = \dfrac{a(s-b)}{c-b}. \)

A vizsgált \(\displaystyle x=y\) feltételt rendezve:

\(\displaystyle x = y, \)

\(\displaystyle \frac{c(s-a)(s-b)}{(s-a)(s-b)-(s-c)^2} = \dfrac{a(s-b)}{c-b}, \)

\(\displaystyle c(s-a)(c-b)-a\big((s-a)(s-b)-(s-c)^2\big) = 0, \)

\(\displaystyle 2c(b+c-a)(c-b)-a\big((b+c-a)(a+c-b)-(a+b-c)^2\big) = 0, \)

\(\displaystyle 2(a^3+a^2c+ab^2-ac^2-b^2+c^3) = 0, \)

\(\displaystyle 2(a-c)(a^2+b^2-c^2) = 0. \)

A feltétel szerint \(\displaystyle a<c\), így \(\displaystyle x=y\) akkor és csak akkor teljesül, ha \(\displaystyle a^2+b^2=c^2\).

Statistics:

38 students sent a solution.
5 points:	Bencsik Dávid, Bényei Borisz, Chrobák Gergő, Csilling Dániel, Csonka Illés, Farkas 512 Izabella, Fülöp Csilla, Kalocsai Zoltán, László Anna, Mohay Lili Veronika, Nagy 551 Levente, Németh Márton, Nguyen Kim Dorka, Rareș Polenciuc, Romaniuc Albert-Iulian, Somogyi Dalma, Szalontai Júlia, Tarján Bernát, Tran Dávid, Varga Boldizsár, Virág Rudolf, Wiener Anna, Zömbik Barnabás.
4 points:	Bognár 171 András Károly, Christ Miranda Anna, Diaconescu Tashi, Lovas Márton.
3 points:	3 students.
2 points:	6 students.
1 point:	1 student.
0 point:	1 student.

Problems in Mathematics of KöMaL, November 2021