Problem B. 5205. (November 2021)

B. 5205. There are four circles given in the plane: circle \(\displaystyle k_2\) lies in the interior of circle \(\displaystyle k_1\), circle \(\displaystyle k_3\) lies in the interior of \(\displaystyle k_2\), and circle \(\displaystyle k_4\) lies in the interior of \(\displaystyle k_3\). Also given are three lines \(\displaystyle e_1\), \(\displaystyle e_2\) and \(\displaystyle e_3\) which are pairwise non-parallel and each line intersects each circle. For all \(\displaystyle i=1,2,3\) let the intersections of line \(\displaystyle e_i\) with the circles be \(\displaystyle A_i\), \(\displaystyle B_i\), \(\displaystyle C_i\), \(\displaystyle D_i\), \(\displaystyle E_i\), \(\displaystyle F_i\), \(\displaystyle G_i\) and \(\displaystyle H_i\), in this order. Prove that if \(\displaystyle A_1B_1+E_1F_1=C_1D_1+G_1H_1\) and \(\displaystyle A_2B_2+E_2F_2=C_2D_2+G_2H_2\) then \(\displaystyle A_3B_3+E_3F_3=C_3D_3+G_3H_3\).

(6 pont)

Deadline expired on December 10, 2021.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A megoldáshoz az \(\displaystyle A_iB_i+E_iF_i=C_iD_i+G_iH_i\) feltételt átfogalmazzuk egy, a körök középpontjaira vonatkozó állításra. Jelölje a \(\displaystyle k_j\) kör középpontját \(\displaystyle O_j\) (\(\displaystyle j=1,2,3,4\)), és legyen \(\displaystyle \mathbf{w}=\overrightarrow{O_1O_2}+\overrightarrow{O_4O_3}\).

Lemma. Bármely \(\displaystyle i=1,2,3\) esetén \(\displaystyle A_iB_i+E_iF_i=C_iD_i+G_iH_i\) akkor és csak akkor teljesül, ha a \(\displaystyle \mathbf{w}\) vektor merőleges az \(\displaystyle e_i\) egyenesre.

Bizonyítás. Mivel az \(\displaystyle A_i,\ldots,H_i\) pontok ebben a sorrendben helyezkednek el az \(\displaystyle e_i\) egyenesen, az \(\displaystyle A_iB_i+E_iF_i=C_iD_i+G_iH_i\) feltétel ekvivalens azzal, hogy \(\displaystyle \overrightarrow{A_iB_i}+\overrightarrow{E_iF_i} = \overrightarrow{C_iD_i}+\overrightarrow{G_iH_i}\). Legyen \(\displaystyle \mathbf{h}_i=\overrightarrow{A_iB_i}+\overrightarrow{E_iF_i}-\overrightarrow{C_iD_i}-\overrightarrow{G_iH_i}\); azt kell vizsgálnunk, hogy \(\displaystyle \mathbf{h}_i\) mikor a nullvektor. A \(\displaystyle \mathbf{h}_i\) vektor a defníciója miatt párhuzamos az \(\displaystyle e_i\) egyenessel, ezért akkor és csak akkor a nullvektor, ha egyben merőleges is \(\displaystyle e_i\)-re.

Mivel a körök a megadott sorrendben tartalmazzák egymást, \(\displaystyle A_i\) és \(\displaystyle H_i\) a legkülső \(\displaystyle k_1\) körön, \(\displaystyle B_i\) és \(\displaystyle G_i\) a \(\displaystyle k_2\), \(\displaystyle C_i\) és \(\displaystyle F_i\) a \(\displaystyle k_3\), \(\displaystyle D_i\) és \(\displaystyle E_i\) pedig a legbelső \(\displaystyle k_4\) körön van. Az \(\displaystyle O_1A_iH_i\), \(\displaystyle O_2B_iG_i\), \(\displaystyle O_3C_iF_i\) és \(\displaystyle O_4D_iE_i\) háromszögek egyenlő szárúak, közös alapegyenesük az \(\displaystyle e_i\), ezért az \(\displaystyle \overrightarrow{O_1A_i}+\overrightarrow{O_1H_i}\), \(\displaystyle \overrightarrow{O_2B_i}+\overrightarrow{O_2G_i}\), \(\displaystyle \overrightarrow{O_3C_i}+\overrightarrow{O_3F_i}\) és \(\displaystyle \overrightarrow{O_4D_i}+\overrightarrow{O_4E_i}\) vektorok merőlegesek \(\displaystyle e_i\)-re. A lemmát úgy igazoljuk, hogy ezek, \(\displaystyle \overrightarrow{O_1O_2}\) és \(\displaystyle \overrightarrow{O_4O_3}\) lineáris kombinációjaként írjuk fel \(\displaystyle \mathbf{h}_i\)-t:

Mint láttuk, az utolsó sorban \(\displaystyle \overrightarrow{O_1A_i}+\overrightarrow{O_1H_i}\), \(\displaystyle \overrightarrow{O_2B_i}+\overrightarrow{O_2G_i}\), \(\displaystyle \overrightarrow{O_3C_i}+\overrightarrow{O_3F_i}\) és \(\displaystyle \overrightarrow{O_4D_i}+\overrightarrow{O_4E_i}\) mind merőleges \(\displaystyle e_i\)-re, ezért \(\displaystyle \mathbf{h}_i\) akkor és csak akkor merőleges \(\displaystyle e_i\)-re, ha \(\displaystyle \mathbf{w}\) is merőleges \(\displaystyle e_i\)-re. Tehát

\(\displaystyle A_iB_i+E_iF_i=C_iD_i+G_iH_i \quad\Leftrightarrow\quad \mathbf{h}_i=\mathbf{0} \quad\Leftrightarrow\quad \mathbf{h}_i\perp e_i \quad\Leftrightarrow\quad \mathbf{w}\perp e_i. \)

Ezzel a lemmát igazoltuk.

A feladat feltételei szerint \(\displaystyle A_1B_1+E_1F_1=C_1D_1+G_1H_1\) és \(\displaystyle A_2B_2+E_2F_2=C_2D_2+G_2H_2\); a lemma szerint ebből következik, hogy a \(\displaystyle \mathbf{w}\) vektor az \(\displaystyle e_1\) és az \(\displaystyle e_2\) egyenesre is merőleges. Mivel \(\displaystyle e_1\) és \(\displaystyle e_2\) különböző irányú, ez csak úgy lehetséges, ha \(\displaystyle \mathbf{w}=\mathbf{0}\) (tehát \(\displaystyle O_1O_2O_4O_3\) egy – esetleg elfajuló – paralelogramma.)

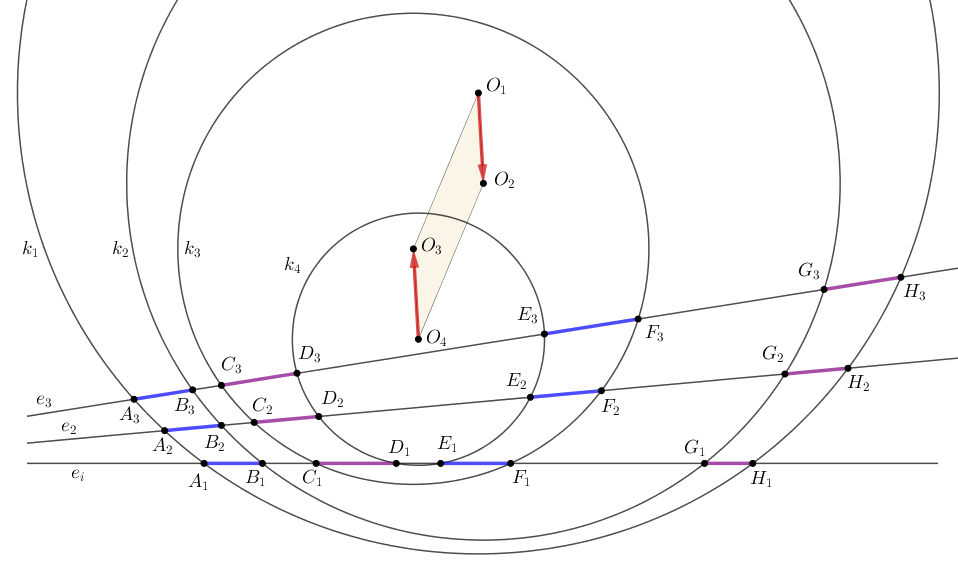
Mivel a \(\displaystyle \mathbf{w}=\mathbf{0}\) vektor az \(\displaystyle e_3\) egyenesre is merőleges, a lemma másik iránya szerint \(\displaystyle A_3B_3+E_3F_3=C_3D_3+G_3H_3\).

Statistics:

26 students sent a solution.
6 points:	Bényei Borisz, Csonka Illés, Kalocsai Zoltán, Mohay Lili Veronika, Németh Márton, Páhán Anita Dalma, Simon László Bence, Somogyi Dalma, Tarján Bernát, Virág Rudolf.
5 points:	Bálint Béla, Bencsik Dávid, Duchon Márton, Lovas Márton, Melján Dávid Gergő, Rareș Polenciuc, Tekes János, Zömbik Barnabás.
4 points:	3 students.
3 points:	2 students.
1 point:	1 student.
0 point:	2 students.

Problems in Mathematics of KöMaL, November 2021