A B. 5208. feladat (2021. december)

B. 5208. Egy kör \(\displaystyle AB\) és \(\displaystyle CD\) húrjai merőlegesek egymásra, a húrok egyenesei a körön kívüli \(\displaystyle P\) pontban metszik egymást; a \(\displaystyle P\)-ből a körhöz húzott érintőszakasz hossza \(\displaystyle e\). Mutassuk meg, hogy az \(\displaystyle AD\) és \(\displaystyle BC\) szakaszok hosszainak mértani közepe legalább \(\displaystyle \sqrt2\, e\).

Javasolta: Kocsis Szilveszter (Budapest)

(4 pont)

A beküldési határidő 2022. január 10-én LEJÁRT.

Megoldás.

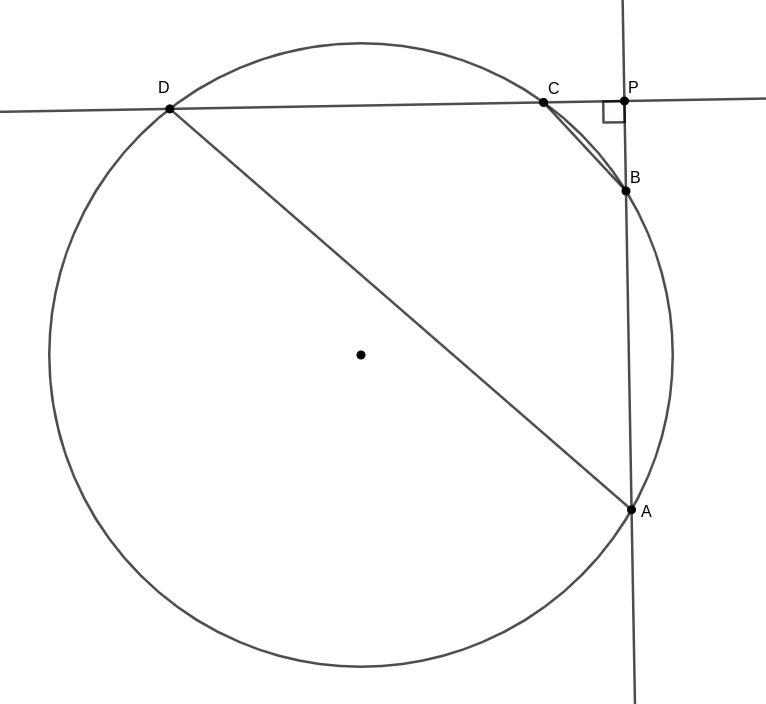
Jelölje az \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) és \(\displaystyle D\) pontok \(\displaystyle P\)-től mért távolságát rendre \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) és \(\displaystyle d\). A külső pontból körhöz húzott szelő- és érintőszakaszok tétele szerint

\(\displaystyle ab=cd=e^2.\)

Az \(\displaystyle AB\) és \(\displaystyle CD\) egyenesek merőlegessége miatt Pitagorasz tételéből kapjuk, hogy

\(\displaystyle AD^2=a^2+d^2 \qquad \text {és} \qquad BC^2=b^2+c^2.\)

Továbbá a számtani és mértani közepek közötti egyenlőtlenség miatt

\(\displaystyle \frac{a^2+d^2}{2}\ge \sqrt{a^2d^2}=ad \qquad \text {és} \qquad \frac{b^2+c^2}{2}\ge \sqrt{b^2c^2}=bc.\)

Így az \(\displaystyle AD\) és \(\displaystyle BC\) szakaszok mértani közepére

\(\displaystyle \sqrt{AD\cdot BC}=\sqrt{\sqrt{a^2+d^2}\cdot \sqrt{b^2+c^2} }\ge\sqrt{\sqrt{2ad}\cdot \sqrt{2bc}}=\sqrt{2\sqrt{abcd}}=\sqrt{2\sqrt{e^4}}=\sqrt 2 e,\)

ezt akartuk igazolni. Egyenlőség pontosan akkor áll, ha \(\displaystyle a=d\) és \(\displaystyle b=c\).

Statisztika:

76 dolgozat érkezett.
4 pontot kapott:	64 versenyző.
3 pontot kapott:	4 versenyző.
2 pontot kapott:	4 versenyző.
0 pontot kapott:	2 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2021. decemberi matematika feladatai