Problem B. 5208. (December 2021)

B. 5208. The lines of two perpendicular chords \(\displaystyle AB\) and \(\displaystyle CD\) of a circle intersect at an exterior point \(\displaystyle P\). The length of the tangent drawn from \(\displaystyle P\) to the circle is \(\displaystyle e\). Show that the geometric mean of the lengths \(\displaystyle AD\) and \(\displaystyle BC\) is at least \(\displaystyle \sqrt2\,e\).

Proposed by Sz. Kocsis, Budapest

(4 pont)

Deadline expired on January 10, 2022.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás.

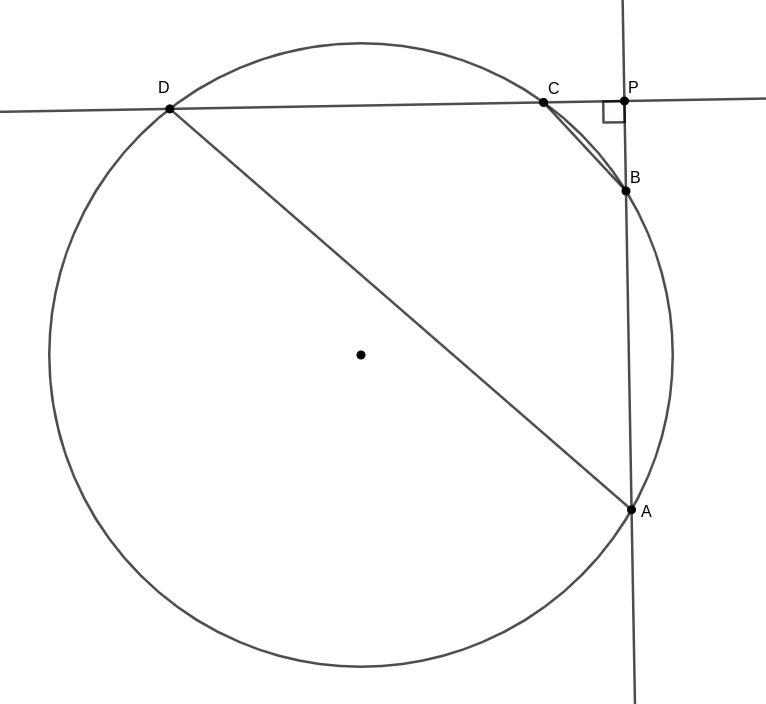
Jelölje az \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\) és \(\displaystyle D\) pontok \(\displaystyle P\)-től mért távolságát rendre \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) és \(\displaystyle d\). A külső pontból körhöz húzott szelő- és érintőszakaszok tétele szerint

\(\displaystyle ab=cd=e^2.\)

Az \(\displaystyle AB\) és \(\displaystyle CD\) egyenesek merőlegessége miatt Pitagorasz tételéből kapjuk, hogy

\(\displaystyle AD^2=a^2+d^2 \qquad \text {és} \qquad BC^2=b^2+c^2.\)

Továbbá a számtani és mértani közepek közötti egyenlőtlenség miatt

\(\displaystyle \frac{a^2+d^2}{2}\ge \sqrt{a^2d^2}=ad \qquad \text {és} \qquad \frac{b^2+c^2}{2}\ge \sqrt{b^2c^2}=bc.\)

Így az \(\displaystyle AD\) és \(\displaystyle BC\) szakaszok mértani közepére

\(\displaystyle \sqrt{AD\cdot BC}=\sqrt{\sqrt{a^2+d^2}\cdot \sqrt{b^2+c^2} }\ge\sqrt{\sqrt{2ad}\cdot \sqrt{2bc}}=\sqrt{2\sqrt{abcd}}=\sqrt{2\sqrt{e^4}}=\sqrt 2 e,\)

ezt akartuk igazolni. Egyenlőség pontosan akkor áll, ha \(\displaystyle a=d\) és \(\displaystyle b=c\).

Statistics:

76 students sent a solution.
4 points:	64 students.
3 points:	4 students.
2 points:	4 students.
0 point:	2 students.
Unfair, not evaluated:	1 solutions.

Problems in Mathematics of KöMaL, December 2021