 Problem B. 5221. (January 2022)
Problem B. 5221. (January 2022)
B. 5221. In an acute-angled triangle \(\displaystyle ABC\), the points of tangency of the inscribed circle on sides \(\displaystyle BC\), \(\displaystyle CA\), \(\displaystyle AB\) are \(\displaystyle D\), \(\displaystyle E\), and \(\displaystyle F\), respectively. The circumscribed circle of the triangle intersects circle \(\displaystyle AEF\) at a point \(\displaystyle P\) different from \(\displaystyle A\), intersects circle \(\displaystyle BFD\) at a point \(\displaystyle Q\) different from \(\displaystyle B\), and intersects circle \(\displaystyle CDE\) at a point \(\displaystyle R\) different from \(\displaystyle C\). Show that the lines \(\displaystyle DP\), \(\displaystyle EQ\) and \(\displaystyle FR\) are concurrent.
Proposed by M. Lovas, Budapest
(6 pont)
Deadline expired on February 10, 2022.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Azt állítjuk, hogy a \(\displaystyle DP\), \(\displaystyle EQ\) és \(\displaystyle FR\) egyenesek átmennek a beírt és a körülírt kör külső hasonlósági pontján. A pontok szerepének szimmetriája miatt elég ezt a \(\displaystyle DP\) egyenesre igazolnunk.

Legyen \(\displaystyle H\) a beírt és a körülírt kör külső hasonlósági pontja, és legyen \(\displaystyle X\) a körülírt kör \(\displaystyle A\)-val szemközti \(\displaystyle BC\) ívének felezőpontja. Azt fogjuk megmutatni, hogy az \(\displaystyle XD\) egyenes a \(\displaystyle P\) és a \(\displaystyle H\) ponton is átmegy; ebből állításunk azonnal következik.
Először megmutatjuk, hogy \(\displaystyle X\), \(\displaystyle D\) és \(\displaystyle P\) egy egyenesen van. Vegyük észre, hogy a \(\displaystyle PBF\) és a \(\displaystyle PCE\) háromszögek hasonlók és azonos körüljárásúak: irányított (modulo \(\displaystyle 180^\circ\)) szögekkel számolva, a kerületi szögek tételéből
\(\displaystyle \angle(BF,PB) = \angle(AB,PB) = \angle(AC,PC) = \angle(CE,PC) \)
és
\(\displaystyle \angle(BF,FP) = \angle(AF,PF) = \angle(AE,PE) = \angle(CE,PE), \)
tehát a két háromszög szögei megegyeznek.
A \(\displaystyle PBF\) és \(\displaystyle PCE\) háromszögek azonos körüljárása miatt a \(\displaystyle P\) pont nem lehet a \(\displaystyle BAC\) szögtartomány belsejében, így \(\displaystyle P\) csak az \(\displaystyle A\)-t is tartalmazó \(\displaystyle CAB\) köríven lehet.
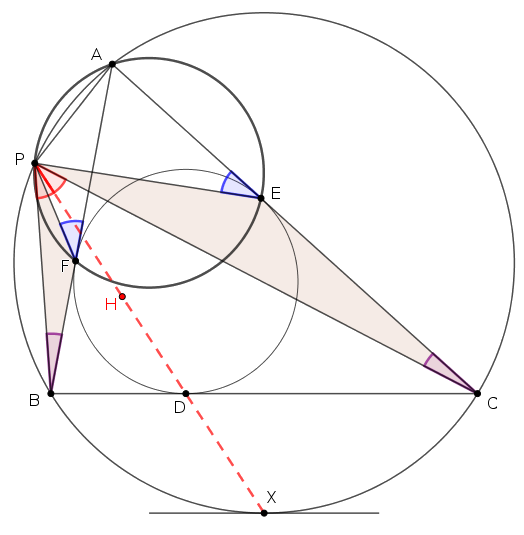
A hasonlóság, valamint \(\displaystyle BD=BF\) és \(\displaystyle CD=CE\) miatt \(\displaystyle \dfrac{PB}{PC} = \dfrac{BF}{CE} = \dfrac{BD}{CD}\); a szögfelezőtétel megfordítása szerint a \(\displaystyle BCP\) háromszögben a \(\displaystyle PD\) szakasz felezi a \(\displaystyle BPC\) szöget; akkor viszont a \(\displaystyle PD\) félegyenes átmegy a \(\displaystyle P\)-vel átellenes, \(\displaystyle A\)-t nem tartalmazó \(\displaystyle BC\) körív felezőpontján, az \(\displaystyle X\) ponton.
Végül megmutatjuk, hogy \(\displaystyle H\), \(\displaystyle D\) és \(\displaystyle X\) is egy egyenesre esik. A \(\displaystyle H\) hasonlósági pontból a beírt kört a körülírt körbe nagyíthatjuk. A beírt kör \(\displaystyle D\)-beli érintője a \(\displaystyle BC\) egyenes, ez párhuzamos a körülírt kör \(\displaystyle X\)-beli érintőjével, és mindkét kör az érintőnek az \(\displaystyle A\)-t tartalmazó oldalán van. Ez viszont azt jelenti, hogy a nagyítás során a \(\displaystyle D\) pont képe éppen az \(\displaystyle X\). Ezért \(\displaystyle H\), \(\displaystyle D\) és \(\displaystyle X\) egy egyenesen van.
Ezzel megmutattuk, hogy \(\displaystyle P\) és \(\displaystyle H\) az \(\displaystyle XD\) egyenesen van, tehát a \(\displaystyle PD\) egyenes átmegy a \(\displaystyle H\) ponton.
Statistics:
23 students sent a solution. 6 points: Baski Bence, Bencsik Dávid, Diaconescu Tashi, Duchon Márton, Kalocsai Zoltán, Kercsó-Molnár Anita, Lovas Márton, Mohay Lili Veronika, Somogyi Dalma, Varga Boldizsár, Virág Rudolf, Wiener Anna. 5 points: Móricz Benjámin, Nagy 429 Leila, Németh Márton. 4 points: 3 students. 3 points: 2 students. 2 points: 1 student. 0 point: 1 student.
Problems in Mathematics of KöMaL, January 2022
