 Problem B. 5226. (February 2022)
Problem B. 5226. (February 2022)
B. 5226. The length of each side of a triangle is at most 2 units. Each pair of vertices is joined with an arc of a unit circle, not longer than a semicircle. Prove that
\(\displaystyle a'+b'>2c'/3, \)
where \(\displaystyle a'\), \(\displaystyle b'\), \(\displaystyle c'\) denote the lengths of the arcs.
(5 pont)
Deadline expired on March 10, 2022.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Először is idézzük fel, hogy az arkuszszinusz függvény a \(\displaystyle [0,1]\) intervallumon konvex, azaz bármely \(\displaystyle x_1,x_2\in [0,1]\) esetén
\(\displaystyle \frac{\arcsin x_1+\arcsin x_2}{2}\ge \arcsin \frac{x_1+x_2}{2}.\)
Másodszor megmutatjuk, hogy \(\displaystyle \arcsin x\ge \arcsin (2x)/3 \) minden \(\displaystyle 0< x \le 1/2\) esetén. A \(\displaystyle 0<x\le 1/2\) feltételből azonnal következik, hogy \(\displaystyle x\ge 4x^3\). Ebből \(\displaystyle 3x-4x^3\ge 2x\), és felhasználva a jól ismert \(\displaystyle \sin 3\varphi= 3\sin \varphi -4\sin^3 \varphi\) azonosságot kapjuk, hogy
\(\displaystyle \sin(3 \arcsin x) = 3 \sin(\arcsin x)- 4 (\sin (\arcsin x))^3=3x-4x^3\ge 2x = \sin (\arcsin 2x). \)
Mivel az arkuszszinusz szigorúan monoton növő, így \(\displaystyle 3\arcsin x\ge \arcsin 2x\) következik, ahogy állítottuk.
Ezután rátérünk a feladat megoldására. Legyenek az oldalak rendre \(\displaystyle 2a\), \(\displaystyle 2b\) és \(\displaystyle 2c\), és tegyük fel, hogy a berajzolt körívek hossza rendre \(\displaystyle 2\alpha\), \(\displaystyle 2\beta\) és \(\displaystyle 2\gamma\), azaz az oldalak a körívek középpontjaiból rendre \(\displaystyle 2\alpha\), \(\displaystyle 2\beta\) és \(\displaystyle 2\gamma\) szög alatt látszanak (ha a középpont illeszkedik valamely oldalra, akkor a megfelelő látószög \(\displaystyle \pi\)). Ekkor
\(\displaystyle \sin \alpha =a \quad ; \quad \sin \beta =b \quad; \quad \sin \gamma =c .\)
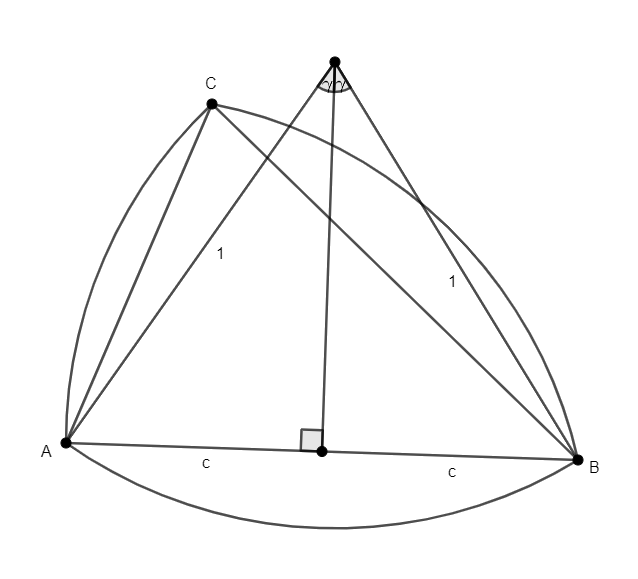
Így a bizonyítandó \(\displaystyle 2\alpha +2\beta > 4\gamma /3\) állítás az
\(\displaystyle \arcsin a+ \arcsin b> \frac 23 \arcsin c\)
ekvivalens alakban írható. Felhasználva az \(\displaystyle a+b>c\) háromszög-egyenlőtlenséget, valamint az arkuszszinusz függvény már említett szigorú monotonitását és konvexitását adódik, hogy
\(\displaystyle \arcsin a+ \arcsin b\ge 2 \arcsin\left (\frac {a+b}{2} \right )> 2 \arcsin\left (\frac {c}{2} \right )\ge \frac 23 \arcsin c,\)
ahol az utolsó becslésnél a második előrebocsájtott észrevételünket használtuk (valamint a \(\displaystyle 0<c/2\le 1/2\) nyilvánvalóan teljesülő összefüggést). Ezzel az állítást beláttuk.
Statistics:
29 students sent a solution. 5 points: Bényei Borisz, Chrobák Gergő, Diaconescu Tashi, Duchon Márton, Farkas 512 Izabella, Fazokán Marcell, Kalocsai Zoltán, Lovas Márton, Mohay Lili Veronika, Móricz Benjámin, Nagy 551 Levente, Németh Márton, Szakács Ábel, Szanyi Attila, Tarján Bernát, Wiener Anna, Zömbik Barnabás. 4 points: Varga Boldizsár. 3 points: 2 students. 2 points: 3 students. 1 point: 3 students. 0 point: 3 students.
Problems in Mathematics of KöMaL, February 2022
