Problem B. 5237. (March 2022)

B. 5237. In a triangle, \(\displaystyle r\) denotes the inradius, \(\displaystyle R\) is the circumradius, and \(\displaystyle s\) denotes the semiperimeter. Prove that if \(\displaystyle r+2R=s\) then the triangle is right angled.

Proposed by R. Fridrik, Szeged

(6 pont)

Deadline expired on April 11, 2022.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Használjuk a szokásos jelöléseket, legyenek a csúcsokból a beírt körhöz húzott érintőszakaszok \(\displaystyle x=s-a\), \(\displaystyle y=s-b\) és \(\displaystyle z=s-c\). Ekkor \(\displaystyle s=x+y+z\), valamint a jól ismert Héron-képlet a \(\displaystyle T=\sqrt{xyz(x+y+z)}\) alakot ölti. Felhasználjuk még az

\(\displaystyle r=\frac{T}{s}=\sqrt{\frac{xyz}{x+y+z}} \quad \text{és} \quad R=\frac{abc}{4T}=\frac{(x+y)(x+z)(y+z)}{4rs}\)

összefüggéseket (többféle alakjukban).

Először egy segédállítást igazolunk.

Segédállítás.

\(\displaystyle r(xy+xz+yz)-xyz=r^3-r^2s+4Rr^2.\)

Ennek igazolásához szorozzuk meg az állítás mindkét oldalát \(\displaystyle s\)-sel:

\(\displaystyle rs(xy+xz+yz)-xyzs=r^3s-r^2s^2+r\cdot4rRs.\)

Ebbe beírva a fentiekből azonnal következő \(\displaystyle 4rRs=(x+y)(x+z)(y+z)\) összefüggést:

\(\displaystyle T(xy+xz+yz)-T^2=r^2T-T^2+\frac{T}{s}\cdot (x+y)(x+z)(y+z).\)

Mindkét oldalhoz \(\displaystyle T^2\)-t adva, majd \(\displaystyle T\)-vel osztva:

\(\displaystyle xy+xz+yz=\frac{xyz}{x+y+z}+\frac{(x+y)(x+z)(y+z)}{x+y+z}.\)

Ez átszorzással és a zárójelek felbontásával könnyen ellenőrizhető azonosság, s mivel ekvivalens átalakításokat végeztünk, így a segédállítást beláttuk.

Most számítsuk ki a segédállítás segítségével az \(\displaystyle (r-x)(r-y)(r-z)\) szorzatot:

\(\displaystyle (r-x)(r-y)(r-z)=r^3-r^2(x+y+z)+r(xy+xz+yz)-xyz=r^3-r^2s+r^3-r^2s+4Rr^2=2r^2(r+2R-s)=0\)

a feltétel szerint. Mivel \(\displaystyle x\), \(\displaystyle y\) és \(\displaystyle z\) szerepe szimmetrikus, így feltehető, hogy \(\displaystyle r-x=0\), azaz \(\displaystyle r=x\).

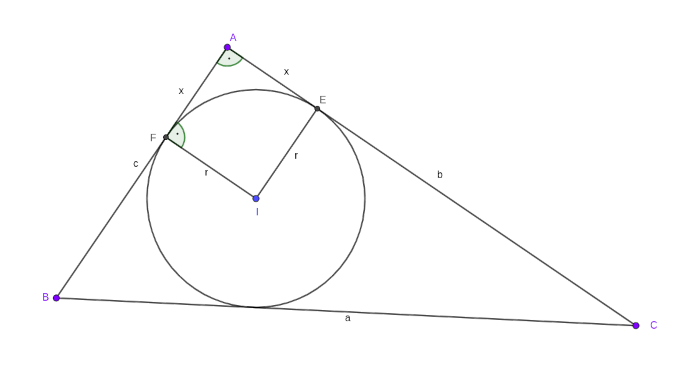
Így az ábrán lévő \(\displaystyle AFIE\) négyszög derékszögű rombusz, azaz négyzet, ami miatt az \(\displaystyle ABC\) háromszög \(\displaystyle A\)-nál levő szöge derékszög. Ezzel az állítást beláttuk.

Megjegyzés. A megoldásban az \(\displaystyle x\), \(\displaystyle y\) és \(\displaystyle z\) érintőszakaszok segítségével kifejeztük az \(\displaystyle r\), \(\displaystyle R\) és \(\displaystyle s\) adatokat. Ezeket visszaírva a feltételbe rendezés, négyzetreemelés majd nullára rendezés után egy hatodfokú, háromváltozós, homogén polinomot kapunk. Direkt számolással ellenőrizhető, hogy ez a polinom \(\displaystyle (x^2+xy+xz-yz)(y^2+xy+yz-xz)(z^2+xz+yz-xy)\) szorzatalakban írható. Szintén direkt számolás mutatja, hogy

\(\displaystyle (x^2+xy+xz-yz)(y^2+xy+yz-xz)(z^2+xz+yz-xy)=\frac{(a^2+b^2-c^2)(a^2+c^2-b^2)(b^2+c^2-a^2)}{8}.\)

Ezekből és a Pitagorasz-tétel megfordításából az állítás következik.

Statistics:

33 students sent a solution.
6 points:	Bényei Borisz, Chrobák Gergő, Diaconescu Tashi, Duchon Márton, Fülöp Csilla, Horváth 530 Mihály, Jánosik Máté, Koleszár Domonkos, Lovas Márton, Mohay Lili Veronika, Nagy 551 Levente, Németh Márton, Romaniuc Albert-Iulian, Simon László Bence, Somogyi Dalma, Tarján Bernát, Tran Dávid, Varga Boldizsár, Veres Dorottya, Virág Rudolf, Wiener Anna, Zömbik Barnabás.
5 points:	Bencsik Dávid, Csonka Illés, Kalocsai Zoltán.
4 points:	1 student.
2 points:	5 students.
1 point:	1 student.
0 point:	1 student.

Problems in Mathematics of KöMaL, March 2022