 |
A B. 5245. feladat (2022. április) |
B. 5245. \(\displaystyle a)\) Bizonyítsuk be, hogy végtelen sok, páronként nem hasonló háromszög létezik, melynek mindhárom oldala egész szám, és az egyik szöge 3-szor akkora, mint egy másik.
\(\displaystyle b)\) A fenti tulajdonságú háromszögek között van-e olyan, amelynek mindhárom oldala legfeljebb 10?
Hujter Mihály (Budapest) ötlete alapján
(6 pont)
A beküldési határidő 2022. május 10-én LEJÁRT.
Megoldás. A megoldásunk kulcsa egy alább kimondott és bizonyított tétel. Teljes megoldást kap az olvasó, ha csak a tétel kimondásánál kezdi az olvasást – a megoldás addigi része a tétel egy lehetséges motivációját (hogyan lehet erre rájönni?) írja le.
Tekintsünk egy olyan \(\displaystyle ABC\) háromszöget, amelynek \(\displaystyle A\)-nál fekvő belső szöge \(\displaystyle \alpha\), míg \(\displaystyle B\)-nél fekvő belső szöge \(\displaystyle 3 \alpha\).
Húzzuk be \(\displaystyle AB\) felezőmerőlegesét, ez messe \(\displaystyle P\) pontban az \(\displaystyle AC\) oldalt. Ekkor egyrészt az \(\displaystyle ABP\) háromszög egyenlő szárú, így \(\displaystyle ABP \sphericalangle = \alpha\). Másrészt ekkor \(\displaystyle CBP \sphericalangle = BPA \sphericalangle = 2 \alpha\) (előbbit \(\displaystyle 3\alpha - \alpha\) külünbségként, utóbbit az \(\displaystyle ABP\) háromszög külső szögeként kapjuk), tehát a \(\displaystyle PBC\) háromszög is egyenlőszárú.
Vezessük be az \(\displaystyle x = AP = PB\), \(\displaystyle y = AB\), \(\displaystyle z=PC = CB\) jelöléseket.
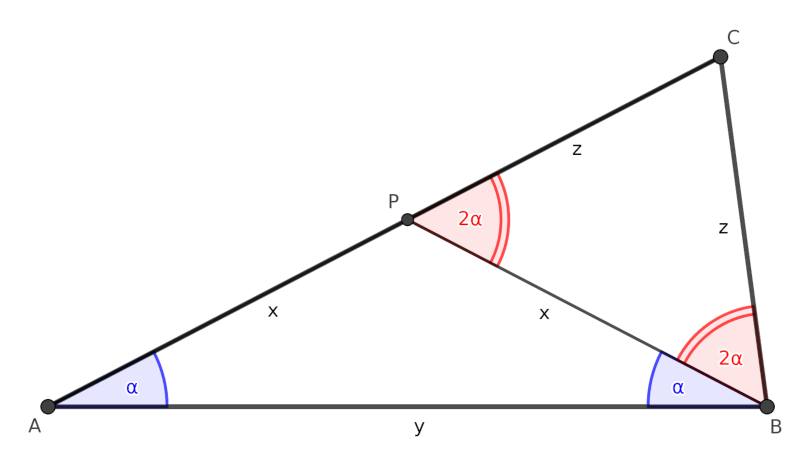
Az \(\displaystyle ABP\) egyelő szárú háromszögben \(\displaystyle x \cdot \cos \alpha = \frac{y}{2}\), azaz \(\displaystyle \cos \alpha = \frac{y}{2x}\).
Hasonlóan, a \(\displaystyle PBC\) egyelő szárú háromszögben \(\displaystyle z \cdot \cos(2 \alpha) = \frac{x}{2}\), azaz:
\(\displaystyle z = \frac{x}{2 \cos(2\alpha)} = \frac{x}{2 \left(2 \cos^2(\alpha) - 1\right)} = \frac{x}{2 \left(2\left(\frac{y}{2x}\right)^2 -1 \right)} = \frac{x}{2 \cdot \dfrac{2y^2-4x^2}{4x^2}} = \frac{x^3}{y^2-2x^2 } \)
Tehát az \(\displaystyle ABC\) háromszög oldalai:
\(\displaystyle AB = y, \qquad BC = z = \frac{x^3}{y^2-2x^2 }, \qquad CA = x + z = \frac{x (y^2-2x^2) + x^3}{y^2-2x^2 } = \frac{xy^2 - x^3}{y^2-2x^2 }. \)
A hasonlóság tulajdonságai szerint persze abban az \(\displaystyle A'B'C'\) háromszögben is teljesül, hogy \(\displaystyle A'B'C'\sphericalangle = 3 \cdot C'A'B' \sphericalangle\), amelynek oldalai az előző \(\displaystyle ABC\) háromszög \(\displaystyle (y^2-2x^2)\)-szeresei, azaz:
\(\displaystyle A'B' = y^3-2x^2y, \qquad B'C' = x^3, \qquad C'A' = xy^2-x^3. \)
Az eddigi gondolatmenetünket megfordítva kapjuk a következő (a megoldás kulcsát jelentő) tételt:
Tétel. Ha \(\displaystyle p\) és \(\displaystyle q\) olyan pozitív valós számok, amelyekre \(\displaystyle \sqrt{2} < q/p < 2\), akkor az
\(\displaystyle AB = q^3-2p^2q, \qquad BC = p^3, \qquad CA = pq^2-p^3 \)
oldalhosszúságok egy olyan háromszöget határoznak meg, amelyben \(\displaystyle ABC\sphericalangle = 3 \cdot CAB \sphericalangle\).
A tétel bizonyítása. A \(\displaystyle q/p > \sqrt{2}\) feltétel miatt \(\displaystyle q^2 > 2p^2\), azaz
\(\displaystyle AB = q^3-2p^2q = q(q^2-2p^2) > 0 \quad \text{és} \quad CA = pq^2 - p^3 = p(q^2-p^2) > 0; \)
tehát valóban pozitív értékeket adtunk meg oldalhosszúságként. (A háromszög-egyenlőtlenséget nem közvetlenül ellenőrizzük le, hanem máshogyan igazoljuk az ilyen oldalhosszúságú háromszög létezését.)
Vegyünk fel egy olyan \(\displaystyle APB\) háromszöget, amelyben \(\displaystyle AB = q^3-2p^2q\), míg
\(\displaystyle AP = PB = \frac{p}{q} \cdot AB = pq^2 - 2p^3.\)
Mivel \(\displaystyle AP + PB = 2 \cdot \frac{p}{q} \cdot AB > AB\), ezért teljesül a háromszög-egyenlőtlenség, tehát létezik ilyen háromszög.
Ezután az \(\displaystyle APB\) háromszög \(\displaystyle PB\) oldalára kifelé felveszünk egy olyan \(\displaystyle PBC\) egyenlő szárú háromszöget, amelyben \(\displaystyle PC = CB = p^3\). Itt is teljesül a háromszög-egyenlőtlenség:
\(\displaystyle PC + CB > PB \Leftrightarrow p^3 + p^3 > pq^2 - 2p^3 \Leftrightarrow 4p^3 > pq^2 \Leftrightarrow 4p^2 > q^2 \Leftrightarrow 2p > q. \)
(Ha két oldal egyenlő, akkor elegendő a ,,szár \(\displaystyle +\) szár \(\displaystyle >\) alap'' típusú egyenlőtlenséget ellenőrizni;
hiszen a ,,szár \(\displaystyle +\) alap \(\displaystyle >\) szár'' egyenlőtlenségek triviálisan teljesülnek.)
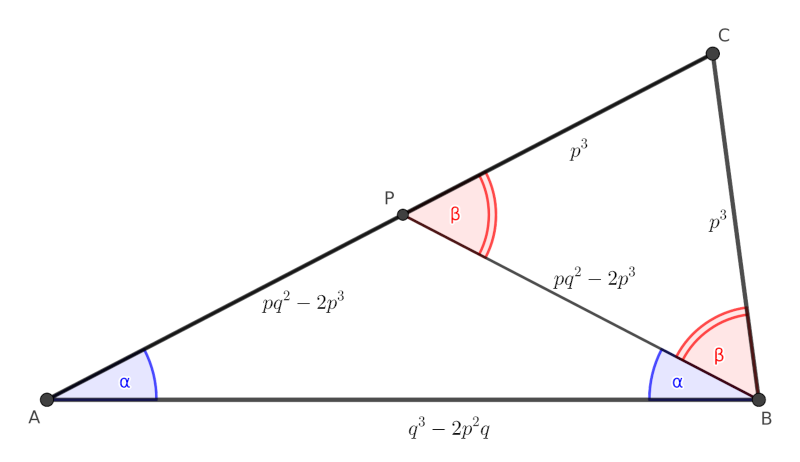
Ezen a ponton tehát van egy olyan \(\displaystyle ABC\) háromszögünk, amelyben az \(\displaystyle AB\) és \(\displaystyle BC\) oldal hossza megfelel a tételben előírtaknak. A \(\displaystyle CA\) oldal hosszának meghatározásához be kell látnunk, hogy \(\displaystyle AP\) és \(\displaystyle PC\) egy egyenesbe esik.
Legyen \(\displaystyle PAB\sphericalangle = ABP\sphericalangle = \alpha\), ekkor
\(\displaystyle \cos \alpha = \frac{AB}{2 \cdot AP} = \frac{q}{2p}. \)
Hasonlóan legyen \(\displaystyle CPB\sphericalangle = PBC\sphericalangle = \beta\), ekkor
\(\displaystyle \cos \beta = \frac{PB}{2 \cdot PC} = \frac{pq^2-2p^3}{2p^3} = \frac{q^2-2p^2}{2p^2} = 2 \frac{q^2}{(2p)^2} -1 = 2 \cos^2 \alpha - 1 = \cos(2 \alpha). \)
Mivel \(\displaystyle \alpha\) és \(\displaystyle \beta\) is hegyesszögek, ezért \(\displaystyle \cos(2 \alpha) = \cos(\beta)\) csak \(\displaystyle 2 \alpha = \beta\) esetén teljesülhet. Ez pedig éppen azt jelenti, hogy:
- \(\displaystyle A,P\) és \(\displaystyle C\) egy egyenesbe esik, hiszen \(\displaystyle APB \sphericalangle = 180^\circ - 2\alpha\) és \(\displaystyle BPC \sphericalangle = 2 \alpha\).
- Következésképpen \(\displaystyle AC = AP + PB = pq^2 - 2p^3 + p^3 = pq^2 - p^3\), tehát az \(\displaystyle ABC\) háromszög oldalai megegyeznek a tételben előírt értékekkel. Azaz tényleg létezik háromszög a tételben előírt oldalhosszúságokkal (teljesül a háromszög-egyenlőtlenség).
- \(\displaystyle CBA \sphericalangle = ABP \sphericalangle + PBC \sphericalangle = \alpha + \beta = 3 \alpha\), tehát valóban teljesül a tétel fő állítása is: \(\displaystyle ABC\sphericalangle = 3 \cdot CAB \sphericalangle\).
Ezzel a tételt bebizonyítottuk.
Most térjünk az eredeti feladat bizonyítására.
Az \(\displaystyle a)\) részhez elegendő meggondolnunk, hogy végtelen sokféleképpen tudunk olyan \(\displaystyle p\) és \(\displaystyle q\) relatív prím egész számokat választani, hogy \(\displaystyle \sqrt{2} < q/p < 2\) teljesüljön (például minden \(\displaystyle n\) pozitív egész esetén \(\displaystyle p=2n, q=2n-1\) megfelel). Ezekből a tétel segítségével le tudunk gyártani egy alkalmas háromszöget. Ha \(\displaystyle p\) és \(\displaystyle q\) relatív prímek, akkor mivel \(\displaystyle \cos(\alpha) = \frac{q}{2p}\), ezért az \(\displaystyle \alpha\) hegyesszög értéke különböző az így kapott háromszögekben. Tehát csak úgy lehet két különböző, relatív prím \(\displaystyle (p,q)\) párral gyártott háromszög hasonló, ha többféleképpen is kiválasztható egy háromszoros szögpár a háromszögben (pl. ha a szögek \(\displaystyle \alpha,3\alpha,9\alpha\) vagy \(\displaystyle \alpha,\alpha,3\alpha\) vagy \(\displaystyle \alpha,3\alpha,3\alpha\) valamilyen sorrendben), de ilyenkor is csak véges sok különböző \(\displaystyle (p,q)\) pár adhatja ugyanazt a háromszöget. Tehát a tétel segítségével konstruáltunk végtelen sok, páronként nem hasonló háromszöget, melyekre teljesül, hogy mindegyik oldala egész szám, és az egyik szöge 3-szor akkora, mint egy másik.
A \(\displaystyle b)\) részhez pedig legyen \(\displaystyle p=2\) és \(\displaystyle q=3\), ekkor a
\(\displaystyle AB = q^3-2p^2q = 3, \qquad BC = p^3 = 8, \qquad CA = pq^2-p^3 = 10; \)
tehát van olyan háromszög, amelynek mindhárom oldala legfeljebb 10, és az egyik szöge 3-szor akkora, mint egy másik.
Statisztika:
31 dolgozat érkezett. 6 pontot kapott: Bencsik Dávid, Christ Miranda Anna, Chrobák Gergő, Farkas 512 Izabella, Fülöp Csilla, Guthy Gábor, Kalocsai Zoltán, Kosztolányi Karina, Lovas Márton, Mohay Lili Veronika, Németh Márton, Simon László Bence, Somogyi Dalma, Szanyi Attila, Varga Boldizsár, Wiener Anna. 5 pontot kapott: Bényei Borisz, Csonka Illés, Szakács Ábel, Zömbik Barnabás. 4 pontot kapott: 9 versenyző. 3 pontot kapott: 1 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2022. áprilisi matematika feladatai

