Problem B. 5249. (May 2022)

B. 5249. Let \(\displaystyle T_0\) denote the area of the triangle formed by the points of tangency of the inscribed circle of triangle \(\displaystyle ABC\) on the sides, and let \(\displaystyle T_1\) denote the area of the triangle formed by the centres of the escribed circles. Show that the geometric mean of \(\displaystyle T_0\) and \(\displaystyle T_1\) equals the area of triangle \(\displaystyle ABC\).

Proposed by P. Bártfai

(5 pont)

Deadline expired on June 10, 2022.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Az \(\displaystyle ABC\) háromszög beírt körének érintési pontjai \(\displaystyle A_0\), \(\displaystyle B_0\), \(\displaystyle C_0\), a beírt kör középpontja \(\displaystyle O\), a hozzáírt körök középpontjai \(\displaystyle A_1\), \(\displaystyle B_1\), \(\displaystyle C_1\); az \(\displaystyle A_0B_0C_0\), \(\displaystyle ABC\), \(\displaystyle A_1B_1C_1\) háromszögek körülírt körének sugara rendre \(\displaystyle R_0\), \(\displaystyle R\), illetve \(\displaystyle R_1\).

Először az \(\displaystyle A_0B_0C_0\) és \(\displaystyle ABC\) háromszögek területének arányát határozzuk meg.

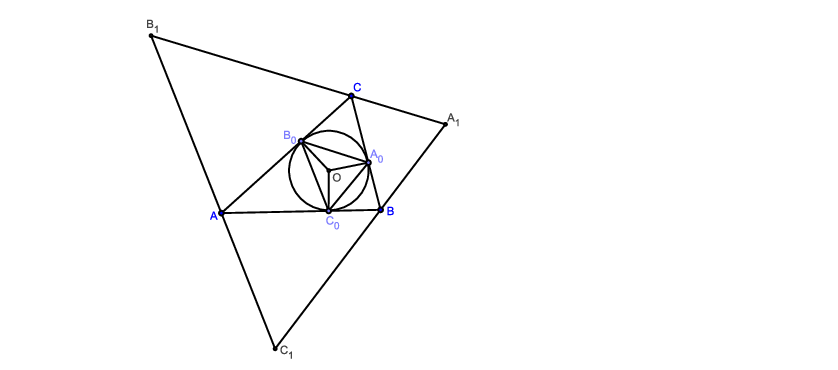
Az érintések miatt például \(\displaystyle OA_0C\sphericalangle=OB_0C\sphericalangle =90^{\circ}\), ezért \(\displaystyle A_0OB_0 \sphericalangle = 180^{\circ}-\gamma\). Nyilván \(\displaystyle T_0\) az \(\displaystyle A_0OB_0\), \(\displaystyle A_0OC_0\), \(\displaystyle B_0OC_0\) háromszögek területének az összege. Például \(\displaystyle A_0OB_0\) területe \(\displaystyle T_{A_0OB_0}= \frac{1}{2}R_0^2\sin (180^{\circ}-\gamma)= \frac{1}{2}R_0^2\sin\gamma\), így

\(\displaystyle T_0 = T_{A_0OB_0} + T_{A_0OC_0} + T_{B_0OC_0} = \frac{1}{2}R_0^2(\sin\alpha + \sin\beta + \sin\gamma). \)

Választása folytán például \(\displaystyle A_1\) illeszkedik a \(\displaystyle B_0AC_0\sphericalangle\) belső szögfelezőjére, ezért \(\displaystyle AA_1\) merőleges \(\displaystyle B_0AC_0\sphericalangle\) külső szögfelezőjére, \(\displaystyle B_1C_1\)-re. Kapjuk, hogy \(\displaystyle ABC\) az \(\displaystyle A_1B_1C_1\) háromszög talpponti háromszöge. Ismeretes, hogy ezért \(\displaystyle A_1B_1C_1\) magasságpontjának az \(\displaystyle A_1B_1C_1\) oldalegyeneseire vonatkozó tükörképei rajta vannak \(\displaystyle A_1B_1C_1\) körülírt körén. Ez azt jelenti, hogy az \(\displaystyle ABC\) háromszöget az \(\displaystyle A_1B_1C_1\) magasságpontjából 2-szeresére nagyítva, a kapott háromszög csúcsai \(\displaystyle A_1B_1C_1\) körülírt körére esnek; így \(\displaystyle R_1=2R\).

Az \(\displaystyle ABC\) háromszög területe:

\(\displaystyle T= \frac{1}{2}R_0(a+b+c) = \frac{1}{2}R_0 (2R \sin \alpha + 2R \sin \beta + 2R \sin \gamma), \)

ezért

\(\displaystyle T/T_0 = \frac{R_0R (\sin \alpha + \sin \beta + \sin \gamma)}{\frac{1}{2}R_0^2(\sin\alpha + \sin\beta + \sin\gamma)} = \frac{2R}{R_0}. \)

Végül megmutatjuk, hogy az \(\displaystyle A_1B_1C_1\) és \(\displaystyle A_0B_0C_0\) háromszögek hasonlóak. Például

\(\displaystyle B_0A_0C_0\sphericalangle = 180^{\circ} - (CA_0B_0\sphericalangle + BA_0C_0\sphericalangle) = 180^{\circ} - ((90^{\circ}-\frac{\gamma}{2}) + (90^{\circ}-\frac{\beta}{2}) ) = \frac{\beta}{2} + \frac{\gamma}{2} = 90^{\circ}-\frac{\alpha}{2}, \)

és

\(\displaystyle B_1A_1C_1\sphericalangle = CA_1B\sphericalangle = 180^{\circ} - (BCA_1\sphericalangle + A_1BC\sphericalangle ) = \)

\(\displaystyle =180^{\circ} -( \frac{180^{\circ}- \gamma}{2} + \frac{180^{\circ}- \beta}{2}) = \frac{\beta}{2} + \frac{\gamma}{2} = 90^{\circ}-\frac{\alpha}{2} = B_0A_0C_0\sphericalangle . \)

A hasonlóság miatt \(\displaystyle T_1\) úgy aránylik \(\displaystyle T_0\)-hoz, mint a háromszögek köré írható körök sugarának a négyzete:

\(\displaystyle \frac{R_1^2}{R_0^2} = T_1/T_0 = T_1/T \cdot T/T_0 = T_1/T \cdot\frac{2R}{R_0}, \)

ezért valóban

\(\displaystyle T_1/T = \frac{R_1^2/R_0^2}{2R/R_0} = \frac{4R^2/R_0^2}{2R/R_0} = \frac{2R}{R_0} = T/T_0. \)

Statistics:

34 students sent a solution.
5 points:	Bencsik Dávid, Bényei Borisz, Christ Miranda Anna, Chrobák Gergő, Czanik Pál, Diaconescu Tashi, Duchon Márton, Fülöp Csilla, Juhász-Molnár Erik, Kalocsai Zoltán, Kosztolányi Karina, Kovács Benedek Noel, Lovas Márton, Mohay Lili Veronika, Móricz Benjámin, Nguyen Kim Dorka, Richlik Bence, Romaniuc Albert-Iulian, Simon László Bence, Somogyi Dalma, Varga Boldizsár, Virág Rudolf, Wiener Anna, Zömbik Barnabás.
4 points:	Csonka Illés.
3 points:	5 students.
2 points:	2 students.
1 point:	1 student.
0 point:	1 student.

Problems in Mathematics of KöMaL, May 2022