Problem B. 5255. (September 2022)

B. 5255. Vertex \(\displaystyle A\) of a triangle \(\displaystyle ABC\) is reflected about vertex \(\displaystyle B\), \(\displaystyle B\) is reflected about \(\displaystyle C\), and \(\displaystyle C\) is reflected about \(\displaystyle A\). The reflections are points \(\displaystyle C_1\), \(\displaystyle A_1\) and \(\displaystyle B_1\), respectively. Show that there exists a triangle with sides of lengths \(\displaystyle AA_1\), \(\displaystyle BB_1\) and \(\displaystyle CC_1\).

(3 pont)

Deadline expired on October 10, 2022.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A felezőpontra ismert formula szerint \(\displaystyle \overrightarrow{CB}=(\overrightarrow{CA}+\overrightarrow{CC_1})/2\), amiből \(\displaystyle \overrightarrow{CC_1}=2\overrightarrow{CB}-\overrightarrow{CA}\). Hasonlóan láthatjuk, hogy \(\displaystyle \overrightarrow{BB_1}=2\overrightarrow{BA}-\overrightarrow{BC}\) és \(\displaystyle \overrightarrow{AA_1}=2\overrightarrow{AC}-\overrightarrow{AB}\). Ezeket összeadva

\(\displaystyle \overrightarrow{AA_1}+\overrightarrow{BB_1}+\overrightarrow{CC_1}=(2\overrightarrow{CB}-\overrightarrow{CA})+(2\overrightarrow{BA}-\overrightarrow{BC})+(2\overrightarrow{AC}-\overrightarrow{AB}) =3(\overrightarrow{BA}+\overrightarrow{CB}+\overrightarrow{AC})=\mathbf 0.\)

Továbbá vegyük észre, hogy \(\displaystyle \overrightarrow{AA_1}+4\overrightarrow{BB_1}-2\overrightarrow{CC_1}=2\overrightarrow{AC}-\overrightarrow{AB}+8\overrightarrow{BA}-4\overrightarrow{BC}-4\overrightarrow{CB}+2\overrightarrow{CA}=9\overrightarrow{BA}.\) Hasonlóan, \(\displaystyle \overrightarrow{BB_1}+4\overrightarrow{CC_1}-2\overrightarrow{AA_1}=9\overrightarrow{CB}\) és \(\displaystyle \overrightarrow{CC_1}+4\overrightarrow{AA_1}-2\overrightarrow{BB_1}=9\overrightarrow{AC}\). Így \(\displaystyle \overrightarrow{AA_1}\), \(\displaystyle \overrightarrow{BB_1}\) és \(\displaystyle \overrightarrow{CC_1}\) vektorok nem lehetnek egymással párhuzamosak, mert akkor \(\displaystyle ABC\) oldalvektorai is párhuzamosak lennének.

Így \(\displaystyle \overrightarrow{AA_1}\), \(\displaystyle \overrightarrow{BB_1}\) és \(\displaystyle \overrightarrow{CC_1}\) egy nem elfajuló háromszög oldalvektorai, amiből az állítás azonnal következik.

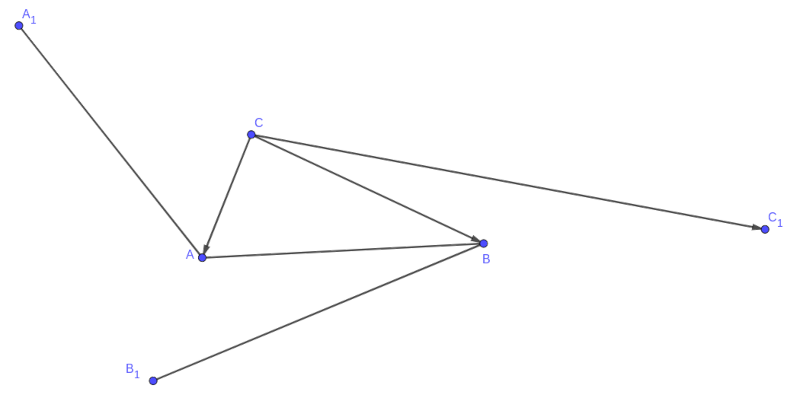
Megjegyzés. Negatív osztási arányt is értelmezve az osztópontba mutató vektorra vonatkozó ismert formula általánosítható arra az esetre, ha az osztópont nem belső pontja a pontok által meghatározott szakasznak, de illeszkedik az egyenesükre. Tulajdonképpen ezt használtuk a megoldásban.

Statistics:

191 students sent a solution.
3 points:	94 students.
2 points:	15 students.
1 point:	5 students.
0 point:	62 students.
Unfair, not evaluated:	6 solutionss.
Not shown because of missing birth date or parental permission:	3 solutions.

Problems in Mathematics of KöMaL, September 2022