 Problem B. 5257. (September 2022)
Problem B. 5257. (September 2022)
B. 5257. In an acute-angled triangle \(\displaystyle ABC\), the heights are \(\displaystyle AA_1\), \(\displaystyle BB_1\), \(\displaystyle CC_1\), and the midpoint of side \(\displaystyle AB\) is \(\displaystyle F\). A circle \(\displaystyle k\) passes through the points \(\displaystyle F\) and \(\displaystyle C_1\), and intersects the extensions of line segments \(\displaystyle A_1C_1\) and \(\displaystyle B_1C_1\) beyond \(\displaystyle C_1\) at points \(\displaystyle P\) and \(\displaystyle Q\), respectively. Prove that \(\displaystyle A_1P=B_1Q\).
(4 pont)
Deadline expired on October 10, 2022.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A feltétel szerint a háromszög hegyesszögű, ezért a magasságok talppontjai az odalak belsejébe esnek.
A feladat állítása pontatlan: ha \(\displaystyle C_1=F\), akkor a \(\displaystyle P\) és \(\displaystyle Q\) pontok helyzete az \(\displaystyle A_1C_1\), illetve \(\displaystyle B_1C_1\) félegyenesen független egymástól. Az állítás akkor marad igaz, ha feltételezzük, hogy a \(\displaystyle C_1=F\) esetben a \(\displaystyle k\) kör érinti az \(\displaystyle AB\) egyenest: ilyenkor a háromszög egyenlő szárú, az ábra szimmetrikus a \(\displaystyle CC_1\) magasságra, az \(\displaystyle A_1P\) és \(\displaystyle B_1Q\) szakaszok egymás tükörképei, így az állítás triviális.
A továbbiakban az általános esetet vizsgáljuk, amikor \(\displaystyle C_1\ne F\), és megmutatjuk, hogy az \(\displaystyle A_1PF\) háromszög egybevágó a \(\displaystyle B_1QF\) háromszöggel; ebből a bizonyítandó állítás, \(\displaystyle A_1P=B_1Q\) azonnal következik.
Mivel az \(\displaystyle A\) és \(\displaystyle B\), \(\displaystyle A_1\) és \(\displaystyle B_1\), valamint \(\displaystyle P\) és \(\displaystyle Q\) felcserélésével ugyenezt az állítást kapnánk, az általánosság csorbítása nélkül feltehetjük, hogy \(\displaystyle C_1\) az \(\displaystyle AF\) szakasznak belső pontja.
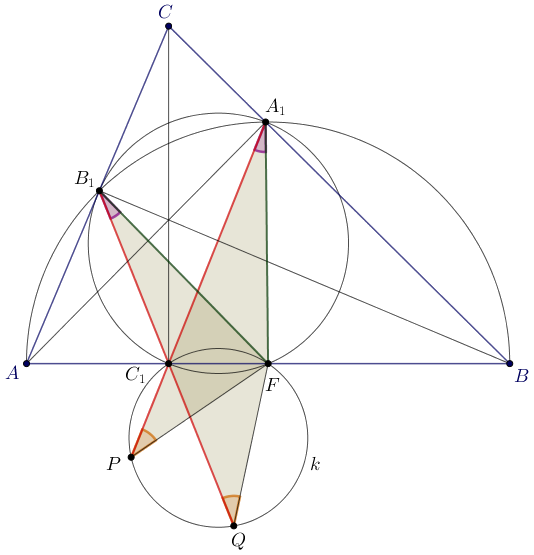
Az \(\displaystyle A_1\) és a \(\displaystyle B_1\) pont a magasságok talppontjai, ezért ezek a pontok az \(\displaystyle AB\) szakasz Thalész-körén vannak. A kör középpontja \(\displaystyle F\); a Thalész-körnek az \(\displaystyle FA_1\) és \(\displaystyle FB_1\) szakaszok sugarai, tehát
| \(\displaystyle FA_1=FB_1. \) | \(\displaystyle (1) \) |
Az \(\displaystyle A_1\), \(\displaystyle B_1\), \(\displaystyle C_1\) és \(\displaystyle F\) pontok egy körön, a háromszög Feuerbach-körén vannak, ezért
| \(\displaystyle PA_1F\sphericalangle = C_1A_1F\sphericalangle = C_1B_1F\sphericalangle = QB_1F\sphericalangle. \) | \(\displaystyle (2) \) |
A feltétel szerint \(\displaystyle FC_1PQ\) a \(\displaystyle k\) körbe írt húrnégyszög, így
| \(\displaystyle FPA_1\sphericalangle = FPC_1\sphericalangle = FQC_1\sphericalangle = FQB_1\sphericalangle. \) | \(\displaystyle (3) \) |
Az (1,2,3) szerint az \(\displaystyle A_1PF\) és a \(\displaystyle B_1QF\) háromszögben egy-egy oldal és két-két megfelelő szög ugyanakkora, tehát a két háromszög egybevágó. Ezzel bebizonyítottuk, hogy az egymásnak megfelelő \(\displaystyle A_1P\), illetve \(\displaystyle B_1Q\) oldalaik is ugyanakkorák.
Statistics:
78 students sent a solution. 4 points: 59 students. 3 points: 6 students. 2 points: 3 students. 1 point: 2 students. 0 point: 5 students.
Problems in Mathematics of KöMaL, September 2022
