 |
A B. 5260. feladat (2022. szeptember) |
B. 5260. A \(\displaystyle k\) kör \(\displaystyle AB\) húrjának \(\displaystyle G\) és \(\displaystyle H\) pontjaira \(\displaystyle AG=GH=HB=1\). A kör egyik \(\displaystyle AB\) ívének felezőpontja legyen \(\displaystyle F\). Az \(\displaystyle FH\) és \(\displaystyle FG\) szelők a kört másodszor a \(\displaystyle C\), illetve \(\displaystyle D\) pontban metszik. Mutassuk meg, hogy \(\displaystyle CD=BC^2\).
Javasolta: Kocsis Szilveszter (Budapest)
(6 pont)
A beküldési határidő 2022. október 10-én LEJÁRT.
1. megoldás. Az \(\displaystyle ABC\) háromszög körülírt köre a megadott \(\displaystyle k\), továbbá a \(\displaystyle CF\) szakasz felezi az \(\displaystyle AB\) ívet, tehát \(\displaystyle CF\) az \(\displaystyle ABC\) háromszög \(\displaystyle C\)-hez tartozó belső szögfelezője.

A szögfelezőtétel alapján így \(\displaystyle AC:BC=AH:HB=2\). Ugyanezekkel a lépésekkel látjuk, hogy \(\displaystyle DF\) pedig az \(\displaystyle ABD\) háromszög \(\displaystyle D\)-hez tartozó belső szögfelezője, vagyis \(\displaystyle BD:AD=GB:AG=2\). Az ábra szimmetrikus az \(\displaystyle AB\) felezőmerőlegesére, ezzel azonnal adódik az is, hogy \(\displaystyle AC=BD=2BC=2AD\). A befejezéshez az \(\displaystyle ABCD\) húrtrapézra alkalmazzuk Ptolemaiosz tételét:
\(\displaystyle AC\cdot BD=BC\cdot AD+AB\cdot CD.\)
Korábbi megállapításaink és annak felhasználásával, hogy \(\displaystyle AB=3\), rendezés után:
\(\displaystyle 2BC\cdot 2BC=BC\cdot BC +3\cdot CD,\)
\(\displaystyle 4\cdot BC^2=BC^2+3\cdot CD,\)
\(\displaystyle BC^2=CD.\)
2. megoldás. A feladatra egy olyan megoldást is mutatunk, amely nem használja az erős Ptolemaiosz-tételt.
Ábránkat és jelöléseinket egészítsük ki a következőkkel:
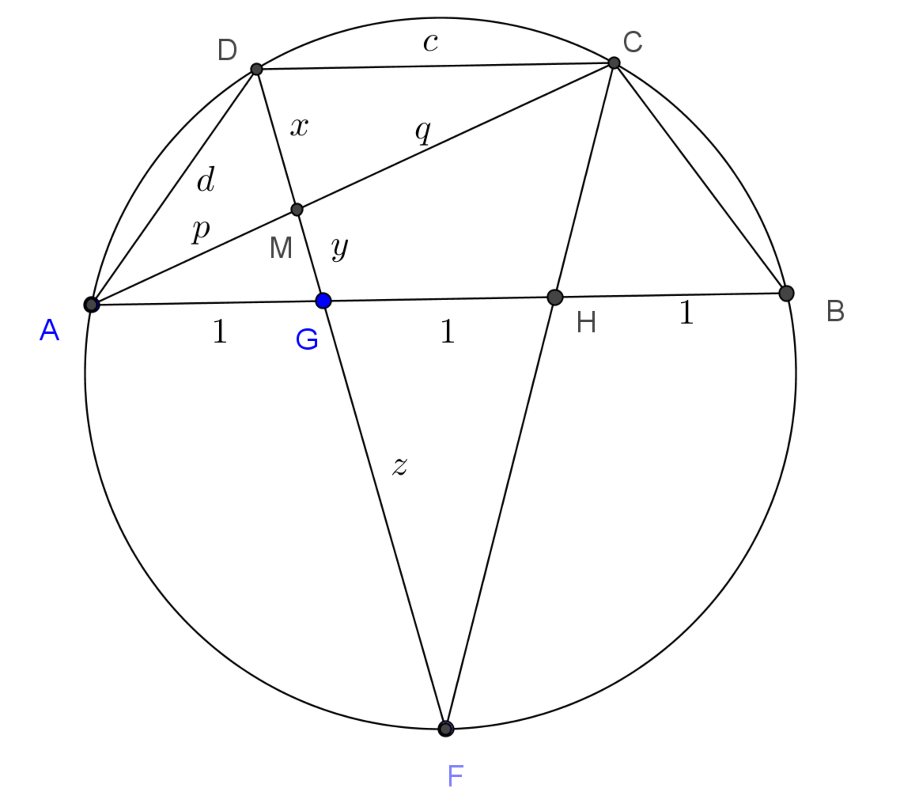
Az \(\displaystyle AC\) és \(\displaystyle DF\) szakaszok metszéspontja \(\displaystyle M\). Az \(\displaystyle AC\) szakaszt az \(\displaystyle M\) pont az \(\displaystyle AM=p\) és \(\displaystyle MC=q\) hosszúságú szakaszokra osztja, továbbá az \(\displaystyle M\) és \(\displaystyle G\) pontok a \(\displaystyle DF\) szakaszt \(\displaystyle x\), \(\displaystyle y\) és \(\displaystyle z\) hosszúságú részekre; \(\displaystyle DM=x\), \(\displaystyle MG=y\), \(\displaystyle GF=z\). A szokásos jelölésekkel a trapéz \(\displaystyle CD\) alapja \(\displaystyle c\), \(\displaystyle AD\) szára pedig \(\displaystyle d\).
Azt kell bizonyítani az egység figyelembevételével, hogy \(\displaystyle d^2=c\).
A következőkben háromszögek hasonlóságánál végig felhasználjuk, hogy \(\displaystyle AG=GH=HB=1\), valamint az ábra szimmetriája alapján azt is, hogy \(\displaystyle ABCD\) szimmetrikus trapéz, \(\displaystyle DC\parallel AB\).
Az \(\displaystyle AB\parallel CD\) miatt \(\displaystyle FGH\triangle \sim FDC\triangle\),
\(\displaystyle \frac{CD}{GH}= \frac{FD}{FG} \quad \Rightarrow \quad \frac{c}{1}=\frac{x+y+z}{z}. \tag{1} \)
Másrészt a \(\displaystyle CD\parallel AG\) miatt \(\displaystyle AMG\triangle \sim CMD\triangle\),
\(\displaystyle \frac{CD}{AG}= \frac{MC}{AM}=\frac{DM}{MG} \quad \Rightarrow \quad \frac{c}{1}=\frac{q}{p}=\frac{x}{y}. \tag{2} \)
Harmadrészt \(\displaystyle AMD\sphericalangle, FMC\sphericalangle\) csúcsszögek, \(\displaystyle ADM\sphericalangle\) és \(\displaystyle MCF\sphericalangle\) az \(\displaystyle AF\) ívhez tartozó kerületi szögek, amelyek miatt \(\displaystyle ADM\triangle \sim FCM\triangle\),
\(\displaystyle \frac{AD}{FC}= \frac{AM}{FM}=\frac{DM}{MC} \quad \Rightarrow \quad \frac{d}{x+y+z}=\frac{p}{y+z}=\frac{x}{q}. \tag{3} \)
A (3)-ból kifejezve \(\displaystyle d^2\)-et:
\(\displaystyle d^2=\frac{(x+y+z)^2x^2}{q^2}.\)
Most (2) alapján \(\displaystyle \frac{x}{q}=\frac{y}{p}\), majd (3)-ból \(\displaystyle \frac{x}{pq}=\frac{1}{y+z}\) beírásával:
\(\displaystyle d^2=\frac{(x+y+z)^2x^2}{q^2}=\frac{(x+y+z)^2xy}{pq}=\frac{(x+y+z)^2xy}{x(y+z)}=\frac{(x+y+z)^2y}{y+z}.\)
Az (1) egyenlőségből \(\displaystyle x+y+z=c\cdot z\), illetve (1) és (4) összevetése alapján \(\displaystyle x+y+z=\frac{xz}{y}\). Írjuk be ezeket is \(\displaystyle d^2\) kifejezésében a számlálóba:
\(\displaystyle d^2=\frac{(x+y+z)^2y}{y+z}=\frac{czy(x+y+z)}{y+z}=\frac{czy\cdot xz}{y(y+z)}=c\cdot \frac{z^2x}{y+z}=c\cdot \frac{xz\cdot z(x+y)}{(y+z)(x+y)}. \)
Ha tekintjük a G pontra vonatkozó szelőtételt a körben, akkor az egységek alapján \(\displaystyle z(x+y)=2\). Vagyis az összes eddigi átalakításokkal:
\(\displaystyle d^2=c\cdot \frac{xz\cdot z(x+y)}{(y+z)(x+y)}=c\cdot \frac{2xz}{(y+z)(x+y)}.\)
Az (1) és (2) összevetése alapján \(\displaystyle xz=y(x+y+z)\), a számláló egyik \(\displaystyle xz\) szorzatát kicserélhetjük a vele egyenló \(\displaystyle y(x+y+z)\)-re:
\(\displaystyle d^2=c\cdot \frac{xz+xz}{(y+z)(x+y)}=c\cdot \frac{xz+y(x+y+z)}{(y+z)(x+y)}=c\cdot \frac{xy+yz+y^2+xz}{xy+yz+y^2+xz}=c. \)
Statisztika:
61 dolgozat érkezett. 6 pontot kapott: Aravin Peter, Bencz Benedek, Bényei Borisz, Bodor Mátyás, Chrobák Gergő, Czanik Pál, Diaconescu Tashi, Duchon Márton, Farkas 005 Bendegúz, Fazokán Marcell, Fehérvári Donát, Fekete Martin, Fodor Dóra, Fodor Gergely, Fórizs Emma, Fülöp Csilla, Gömze Norken, Hetyei Dániel, Horváth 530 Mihály, Jármai Roland, Kosztolányi Karina, Kovács Benedek Noel, Lovas Márton, Melján Dávid Gergő, Miklós Janka, Molnár István Ádám, Nguyen Kim Dorka, Op Den Kelder Ábel, Prohászka Bulcsú, Romaniuc Albert-Iulian, Seprődi Barnabás Bendegúz, Seres-Szabó Márton, Simon László Bence, Sütő Áron, Szakács Ábel, Szalontai Júlia, Szemlér Bálint, Tarján Bernát, Tusnády Sámuel, Varga Boldizsár, Veres Dorottya, Wiener Anna, Zömbik Barnabás. 5 pontot kapott: 10 versenyző. 4 pontot kapott: 3 versenyző. 3 pontot kapott: 2 versenyző.
A KöMaL 2022. szeptemberi matematika feladatai

