 |
A B. 5267. feladat (2022. október) |
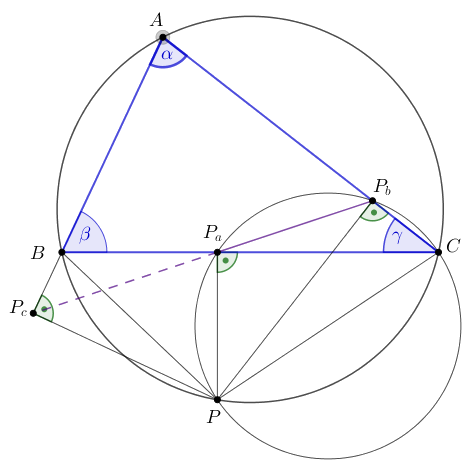
B. 5267. Adott egy \(\displaystyle p\) és egy \(\displaystyle q\) hosszúságú szakasz, valamint egy \(\displaystyle ABC\) háromszög, amelynek oldalegyenesei \(\displaystyle a\), \(\displaystyle b\) és \(\displaystyle c\) a szokásos betűzés szerint. Szerkesszük meg az \(\displaystyle ABC\) körülírt körén azt a \(\displaystyle P\) pontot, amire \(\displaystyle P_a\) a \(\displaystyle P_bP_c\) szakaszt \(\displaystyle p:q\) arányban osztja, ahol \(\displaystyle P_x\) a \(\displaystyle P\) pont merőleges vetülete az \(\displaystyle x\) oldalegyenesre.
(5 pont)
A beküldési határidő 2022. november 10-én LEJÁRT.
Megjegyzés. Jól ismert, hogy ha \(\displaystyle P\) az \(\displaystyle ABC\) háromszög köré írt kör tetszőleges pontja, akkor a \(\displaystyle P_a\), \(\displaystyle P_b\), \(\displaystyle P_c\) pontok egy egyenesen, a háromszög \(\displaystyle P\)-hez tartozó Simson-egyenesén vannak. A \(\displaystyle P_a\), \(\displaystyle P_b\), \(\displaystyle P_c\) pontok sorrendjének vizsgálata óvatos diszkussziót igényel, ugyanis a pontok sokféleképpen helyezkedhetnek el a háromszög oldalain és az oldalak meghosszabbításain. Ha a háromszög tompaszögű, még az is elfordulhat, hogy \(\displaystyle P_a\), \(\displaystyle P_b\) és \(\displaystyle P_c\) egyike sem a háromszög oldalaira esik.
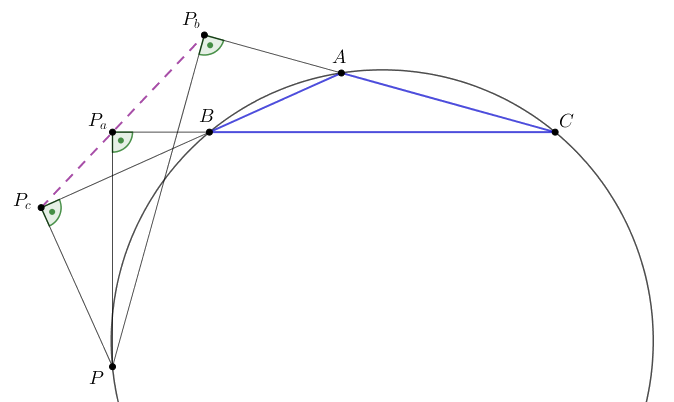
Az itt bemutatott megoldások újra bebizonyítják a Simson-egyenes létezését, meghatározzák \(\displaystyle P_a\), \(\displaystyle P_b\), \(\displaystyle P_c\) pontok sorrendjét és a \(\displaystyle P_aP_b:P_aP_c:P_bP_c\) arányt, és közvetlen módszert biztosítanak a feladatban keresett \(\displaystyle P\) pont szerkesztésére.
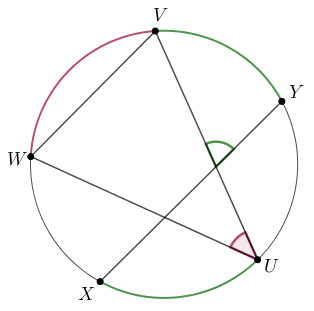
1. megoldás. A megoldás során tetszőleges \(\displaystyle e\) és \(\displaystyle f\) egyenesekre \(\displaystyle \sphericalangle(e,f)\) azt az irányított szöget fogja jelenteni, amellyel el kell forgatnunk az \(\displaystyle e\) egyenest, hogy \(\displaystyle f\)-fel azononos irányú legyen. Ez a szög modulo \(\displaystyle \pi\) értelemben egyértelmű. Válasszuk a körülírt kör átmérőjét távolságegységnek, és a kör tetszőleges \(\displaystyle X\), \(\displaystyle Y\) pontjaira \(\displaystyle \stackrel{\curvearrowright}{XY}\) jelentse az irányított \(\displaystyle XY\) körív hosszát; ez szintén modulo \(\displaystyle \pi\) értelemben egyértelmű. A kerületi és középponti szögek tétele szerint tetszőleges, a körbe írt \(\displaystyle UVW\) háromszögben \(\displaystyle \sphericalangle(UV,UW)\equiv\stackrel{\curvearrowright}{VW}\pmod{\pi}\), és az is ismert, hogy a kör tetszőleges \(\displaystyle UV\) és \(\displaystyle XY\) metsző húrjaira
\(\displaystyle \sphericalangle(XY,UV) \equiv \sphericalangle(XY,UY)+\sphericalangle(UY,UV) \equiv \stackrel{\curvearrowright}{XU}+\stackrel{\curvearrowright}{YV}\pmod{\pi}. \)
Vizsgáljuk először azt az esetet, ha a \(\displaystyle P\) pont az \(\displaystyle A\)-val szemközti \(\displaystyle BC\) körívre esik. Ha \(\displaystyle P=B\) vagy \(\displaystyle P=C\), akkor \(\displaystyle P_a=P_c=B\), illetve \(\displaystyle P_a=P_b=C\), így az is triviális, hogy \(\displaystyle P_a,P_b,P_c\) egy egyenesen van. A következő lépésekben feltesszük, hogy \(\displaystyle P\) a \(\displaystyle BC\) ív belső pontja.
Legyen \(\displaystyle A'\) az \(\displaystyle A\) pont tükörképe a \(\displaystyle BC\) oldal felezőmerőlegesére. Az \(\displaystyle A'\) pont a \(\displaystyle BAC\) köríven van, ezért a \(\displaystyle BC\) és a \(\displaystyle PA'\) húrok metszik egymást; legyen \(\displaystyle Q\) a \(\displaystyle PA'\) és a \(\displaystyle BC\) szakaszok metszéspontja.
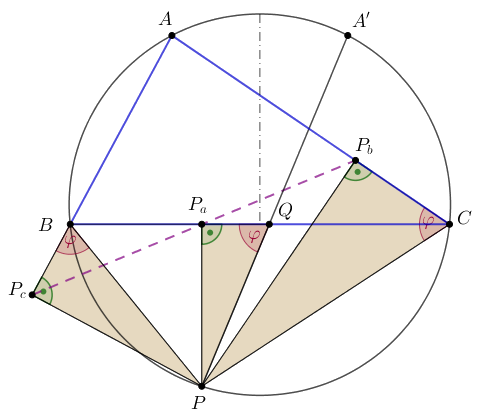
Vegyük észre, hogy az \(\displaystyle ABPC\) húrnégyszögben \(\displaystyle \sphericalangle(BA,BP)\equiv\stackrel{\curvearrowright}{AP}\), \(\displaystyle \sphericalangle(CA,CP)\equiv\stackrel{\curvearrowright}{AP}\) és \(\displaystyle \sphericalangle(CB,A'P) \equiv\stackrel{\curvearrowright}{CA'}+\stackrel{\curvearrowright}{BP} =\stackrel{\curvearrowright}{AB}+\stackrel{\curvearrowright}{BP} =\stackrel{\curvearrowright}{AP}\pmod{\pi}\); az ábrán ezt a szöget jelöltük \(\displaystyle \varphi\)-vel.
Ha \(\displaystyle \varphi\) éppen derékszög, akkor \(\displaystyle P_a=Q\), \(\displaystyle P_b=C\) és \(\displaystyle P_c=B\), ezek a \(\displaystyle BC\) egyenesen vannak.
Ha \(\displaystyle \varphi\) nem derékszög, akkor \(\displaystyle \sphericalangle(BP_c,BP) =\sphericalangle(BA,BP) =\varphi\), \(\displaystyle \sphericalangle(CP_b,CP) =\sphericalangle(CA,CP) =\varphi\) és \(\displaystyle \sphericalangle(QP_a,QP)=\sphericalangle(CB,A'P) =\varphi\). A közös irányított szög miatt a \(\displaystyle PBP_c\), \(\displaystyle PCP_b\) és \(\displaystyle PQP_a\) derékszögű háromszögek hasonlók és azonos körüljárásúak. Az a \(\displaystyle P\) középpontú forgatva nyújtás, amely a \(\displaystyle B\) pontot \(\displaystyle P_c\)-be viszi, egyúttal \(\displaystyle C\)-t \(\displaystyle P_b\)-be, a \(\displaystyle Q\) pontot pedig \(\displaystyle P_a\)-ba viszi. A \(\displaystyle Q\) a \(\displaystyle BC\) szakasz belső pontja, tehát ugyanez igaz a képeikre is: \(\displaystyle P_a\) a \(\displaystyle P_cP_b\) szakasz belső pontja, és \(\displaystyle P_bP_a:P_aP_c=CQ:QB\).
Az \(\displaystyle A,B,C\) csúcsok ciklikus cseréjével ugyanígy láthatjuk, hogy ha \(\displaystyle P\) a \(\displaystyle B\)-vel szemközti \(\displaystyle CA\) íven, vagy a \(\displaystyle C\)-vel szemközti \(\displaystyle AB\) íven van, akkor a Simson-egyenesen a három talppont közül \(\displaystyle P_b\), illetve \(\displaystyle P_c\) van a másik kettő között. Ezért a \(\displaystyle P_b\), \(\displaystyle P_a\), \(\displaystyle P_c\) pontok sorrendje akkor lesz a feladatnak megfelelő, ha \(\displaystyle P\) az \(\displaystyle A\)-val szemközti \(\displaystyle BC\) körív belsejében van. A \(\displaystyle P_bP_a:P_aP_c=p:q\) feltétel pedig akkor teljesül, ha \(\displaystyle BQ:QC=q:p\).
Ezek után a szerkesztés menete:
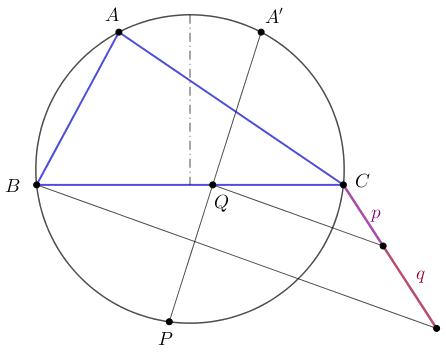
1. Megszerkesztjük a \(\displaystyle BC\) szakaszt \(\displaystyle q:p\) arányban osztó \(\displaystyle Q\) pontot, ezt például az ábra szerint, a párhuzamos szelők tétele segítségével tehetjük meg.
2. Tükrözzük az \(\displaystyle A\) pontot a \(\displaystyle BC\) oldal felezőmerőlegesére, a tükörkép legyen \(\displaystyle A'\).
3. Az \(\displaystyle A'Q\) egyenes és a körülírt kör második, \(\displaystyle A'\)-től különböző metszéspontja a keresett \(\displaystyle P\) pont.
A feladatnak tetszőleges \(\displaystyle ABC\) háromszög és tetszőleges \(\displaystyle p,q>0\) távolságok esetén mindig pontosan egy megoldása van.
2. megoldás. A \(\displaystyle P_aP_b\), \(\displaystyle P_aP_c\), \(\displaystyle P_bP_c\) szakaszok hosszát kifejezzük a háromszög oldalaival és a körülírt kör \(\displaystyle r\) sugarával. Többször felhasználjuk majd a kerületi és középponti szögek tételének azt az egyszerű következményét, hogy \(\displaystyle d\) átmérőjű körben a \(\displaystyle \varphi\) kerületi szöghöz tartozó húr hossza \(\displaystyle d\sin\varphi\).
Legyen a körülírt kör sugara \(\displaystyle r\), a szögei a szokásos betűzéssel \(\displaystyle \alpha\), \(\displaystyle \beta\) és \(\displaystyle \gamma\). Ha \(\displaystyle P\) és \(\displaystyle C\) különböző, akkor a \(\displaystyle P_a\)-nál és \(\displaystyle P_b\)-nél levő derékszögek miatt a \(\displaystyle P_a,P_b\) pontok a \(\displaystyle PC\) átmérőjű körön vannak. Az \(\displaystyle A,C,P_b\) pontok sorrendjétől függően \(\displaystyle P_aCP_b\sphericalangle=\gamma\) vagy \(\displaystyle P_aCP_b\sphericalangle=\pi-\gamma\); ha \(\displaystyle P_b\) és \(\displaystyle C\) egybeesik, akkor pedig a \(\displaystyle C\)-ben húzott \(\displaystyle AC\) érintő zár be \(\displaystyle \gamma\) szöget a \(\displaystyle P_aP_b\) húrral. Mindhárom esetben azt kapjuk, hogy
| \(\displaystyle P_aP_b = PC\cdot\sin P_bCP_a\sphericalangle = PC\cdot\sin\gamma = PC\cdot\dfrac{AB}{2r} = \dfrac{PC\cdot AB}{2r}. \) | \(\displaystyle (1a) \) |
Ha \(\displaystyle P\) és \(\displaystyle C\) egybeesik, akkor \(\displaystyle P_a=P_b=P=C\) és emiatt \(\displaystyle P_aP_b=PC=0\); az (1a) képlet ebben az esetben is igaz.
Hasonlóan kaphatjuk, hogy
| \(\displaystyle P_aP_c = \dfrac{PB\cdot AC}{2r} \quad \text{és} \quad P_bP_c = \dfrac{PA\cdot BC}{2r}. \) | \(\displaystyle (1b) \) |
Az (1a,1b) képletek a \(\displaystyle P_a,P_b,P_c\) pontok sorrendjét is megadják. Ha \(\displaystyle P\) az \(\displaystyle A\)-val szemközti \(\displaystyle BC\) íven van, akkor az \(\displaystyle ABPC\) húrnégyszögre felírhatjuk a Ptolemaiosz-tételt:
\(\displaystyle PB\cdot AC + PC\cdot AB = PA\cdot BC, \)
ezért
\(\displaystyle P_aP_c + P_aP_b = \dfrac{PB\cdot AC}{2r} + \dfrac{PC\cdot AB}{2r} = \dfrac{PA\cdot BC}{2r} = P_bP_c; \)
a háromszög-egyenlőtlenség miatt ez csak úgy lehetséges, ha a \(\displaystyle P_a\) pont a \(\displaystyle P_bP_c\) szakaszon van. Hasonlóan, ha \(\displaystyle P\) a \(\displaystyle B\)-vel szemközti \(\displaystyle CA\) vagy a \(\displaystyle C\)-vel szemközti \(\displaystyle AB\) íven van, akkor \(\displaystyle P_b\), illetve \(\displaystyle P_c\) van a másik két talppont között.
Az (1a,1b) képletek alapján
| \(\displaystyle \dfrac{P_aP_b}{P_aP_c} = \dfrac{PC\cdot AB}{PB\cdot AC}. \) | \(\displaystyle (2) \) |
Tehát, \(\displaystyle P_aP_b:P_aP_c=p:q\) akkor és csak akkor teljesül, ha
| \(\displaystyle \dfrac{PB}{PC} = \dfrac{AB\cdot q}{AC\cdot p}. \) | \(\displaystyle (3) \) |
Ez a tulajdonság egyértelműen meghatározza a \(\displaystyle P\) pont helyét az \(\displaystyle A\)-val szemközti \(\displaystyle BC\) köríven, ezért a feladatnak tetszőleges \(\displaystyle ABC\) háromszög és tetszőleges \(\displaystyle p,q>0\) távolságok esetén mindig pontosan egy megoldása van.
A keresett \(\displaystyle P\) pontot úgy szerkeszthetjük meg, hogy a körülírt kör \(\displaystyle A\)-val szemközti \(\displaystyle BC\) ívét elmetsszük a \(\displaystyle B\) és \(\displaystyle C\) pontokhoz és a \(\displaystyle \dfrac{AB\cdot q}{AC\cdot p}\) arányhoz tartozó Apollóniusz-körrel.
Statisztika:
35 dolgozat érkezett. 5 pontot kapott: Ábrahám Réka, Bényei Borisz, Bodor Mátyás, Chrobák Gergő, Csonka Illés, Czirják Márton Pál, Diaconescu Tashi, Dukát Levente, Elekes Dorottya, Farkas 005 Bendegúz, Fülöp Csilla, Kocsis 827 Péter, Kovács Benedek Noel, Lovas Márton, Melján Dávid Gergő, Nguyen Kim Dorka, Romaniuc Albert-Iulian, Simon László Bence, Szabó 810 Levente, Szakács Ábel, Szalontai Júlia, Tarján Bernát, Tran Dávid, Varga Boldizsár, Veres Dorottya, Virág Lénárd Dániel, Virág Rudolf, Wiener Anna, Zömbik Barnabás. 4 pontot kapott: Csilling Dániel, Horák Zsófia. 3 pontot kapott: 2 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2022. októberi matematika feladatai

