Problem B. 5272. (November 2022)

B. 5272. A flea starts out from point \(\displaystyle (a,b)\) of the coordinate plane, where \(\displaystyle a\), \(\displaystyle b\) are positive integers. With each jump, the flea will move one unit to the left or downwards. It keeps jumping until it reaches either the \(\displaystyle x\) axis or the \(\displaystyle y\) axis. What fraction of the possible sequences of jumps terminate on the \(\displaystyle x\) axis?

Based on the idea of D. Melján, Kecskemét

(4 pont)

Deadline expired on December 12, 2022.

Sorry, the solution is available only in Hungarian. Google translation

1. megoldás. Ha a bolha előbb az \(\displaystyle x\) tengelyt éri el, méghozzá a \(\displaystyle (k,0)\) pontban, akkor oda a \(\displaystyle (k,1)\) pontból érkezett. Amíg az \(\displaystyle (a,b)\) pontból a \(\displaystyle (k,1)\) pontba eljutott, összesen \(\displaystyle a-k\) db balra és \(\displaystyle b-1\) db lefele ugrást végzett. Ilyen ugrássorozatból \(\displaystyle \binom{a+b-k-1}{b-1}\)-féle van (hiszen az \(\displaystyle a+b-k-1\) db egymást követő ugrás közül szabadon kiválaszthatok \(\displaystyle b-1\) db lefele irányulót).

Így az \(\displaystyle x\) tengelyen végződő ugrássorozatok száma:

\(\displaystyle \binom{a+b-2}{b-1} + \binom{a+b-3}{b-1} + \binom{a+b-4}{b-1} + \ldots + \binom{b}{b-1} + \binom{b-1}{b-1}. \)

A Pascal-háromszög közismert ,,zokniszabálya'' (ld. pl.  https://en.wikipedia.org/wiki/ Hockey-stick_identity) szerint ezek összege:

\(\displaystyle \binom{a+b-1}{b}. \)

,,Szimmetrikusan'' ugyanezt elmondhatjuk az \(\displaystyle y\) tengelyen végződő ugrássorozatok számáról, amelyre így \(\displaystyle \binom{a+b-1}{a}\) adódik. Ezen két érték aránya:

\(\displaystyle \frac{\binom{a+b-1}{b}}{\binom{a+b-1}{a}} = \frac{\frac{(a+b-1)!}{(a-1)! \cdot b!}}{\frac{(a+b-1)!}{a! (b-1)!}} = \frac{\frac1{b}}{\frac1{a}} = \frac{a}{b}. \)

Tehát a lehetséges ugrássorozatok \(\displaystyle \dfrac{a}{a+b}\) része végződik az \(\displaystyle x\) tengelyen.

2. megoldás. Utasítsuk a bolhát, hogy miután elérte valamelyik tengelyt, onnan még egyenesen ugráljon el az origóba. Így a bolha összességében egy \(\displaystyle (a,b)\)-ből \(\displaystyle (0,0)\)-ba vezető balra/le ugrássorozatot végez, ezt nevezzük teljes útvonalnak.

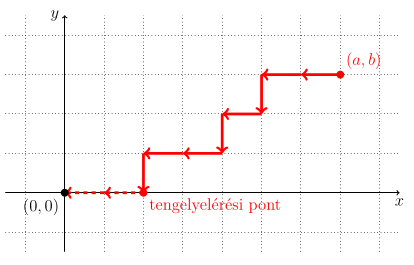
Minden teljes útvonal eléri előbb-utóbb valamelyik tengelyt és a teljes útvonalból egyértelműen rekonstruálható az első tengelyelérésig történő szakasz. Tehát a teljes útvonalak kölcsönösen egyértelműen megfeleltethetők az első tengelyelérésig tartó útvonalaknak.

Teljes útvonalból \(\displaystyle \binom{a+b}{a}\) különböző van, és ezek közül éppen azok érik el előbb az \(\displaystyle x\) tengelyt, mint az \(\displaystyle y\) tengelyt, amelyek az \(\displaystyle (1,0)\) pontból érkeznek az origóba. Az \(\displaystyle (a,b)\)-ből az \(\displaystyle (1,0)\) pontba balra/le lépésekkel \(\displaystyle \binom{a+b-1}{a-1}\)-féleképpen lehet eljutni, így a keresett arány:

\(\displaystyle \frac{\binom{a+b-1}{a-1}}{\binom{a+b}{a}} = \frac{a}{a+b}. \)

Statistics:

128 students sent a solution.
4 points:	55 students.
3 points:	21 students.
2 points:	24 students.
1 point:	5 students.
0 point:	16 students.
Unfair, not evaluated:	4 solutionss.
Not shown because of missing birth date or parental permission:	1 solutions.

Problems in Mathematics of KöMaL, November 2022