Problem B. 5273. (November 2022)

B. 5273. \(\displaystyle D\) is a point on side \(\displaystyle AB\) of an equilateral triangle \(\displaystyle ABC\), and \(\displaystyle E\) is a point on side \(\displaystyle BC\) such that \(\displaystyle \angle BCD =45^\circ\) and \(\displaystyle \angle CDE =30^\circ\). Show that \(\displaystyle BE=2AD\).

Proposed by S. Róka, Nyíregyháza

(4 pont)

Deadline expired on December 12, 2022.

Sorry, the solution is available only in Hungarian. Google translation

1. megoldás. Forgassuk el a \(\displaystyle CAD\) háromszöget a \(\displaystyle C\) csúcs körül \(\displaystyle 60^\circ\)-kal úgy, hogy az \(\displaystyle A\) pont a \(\displaystyle B\) csúcsba kerüljön. Legyen a \(\displaystyle D\) pont elforgatottja a \(\displaystyle D'\) pont.

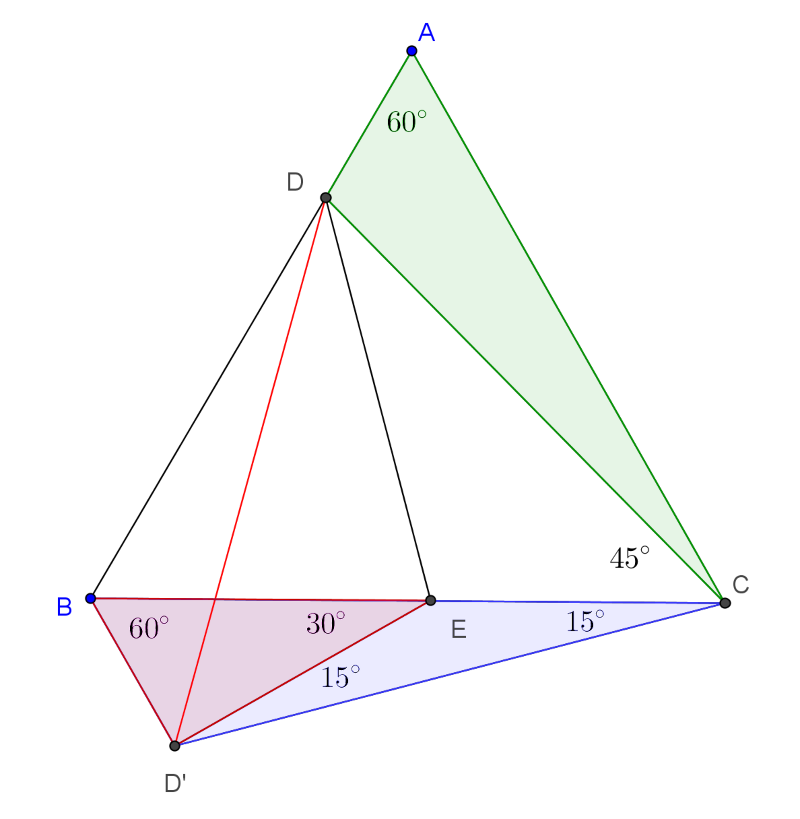
A \(\displaystyle 60^\circ\) forgatás alapján a \(\displaystyle DCD'\) háromszög szabályos, vagyis \(\displaystyle D'DC\sphericalangle=60^\circ\). A feltételben szereplő \(\displaystyle DCB\sphericalangle=45^\circ\) miatt azonnal adódik, hogy \(\displaystyle BCD'\sphericalangle=15^\circ\). A feladat másik feltétele alapján azt is tudjuk, hogy \(\displaystyle CDE\sphericalangle=30^\circ\). Így az \(\displaystyle E\) pont a \(\displaystyle CDD'\) szabályos háromszög belső szögfelezőjére és ezzel együtt a \(\displaystyle D'C\) oldal felezőmerőlegesére illeszkedik. Az \(\displaystyle E\) pont egyenlő távolságra van a \(\displaystyle C\) és \(\displaystyle D'\) pontoktól, a \(\displaystyle CED'\) háromszög egyenlő szárú, \(\displaystyle E\)-nél fekvő külső szöge \(\displaystyle BED'\sphericalangle=30^\circ\). Most tekintsük a \(\displaystyle BD'E\) háromszöget. Ennek \(\displaystyle B\)-nél fekvő szöge \(\displaystyle 60^\circ\), mivel \(\displaystyle DAC\sphericalangle\) elforgatottja, amely pedig az eredeti szabályos háromszög egyik szöge. Szintén a forgatás alapján \(\displaystyle BD'=AD\). A \(\displaystyle BED'\) háromszögnek \(\displaystyle B\)-nél \(\displaystyle 60^\circ\)-os, \(\displaystyle E\)-nél \(\displaystyle 30^\circ\)-os szöge van, ez egy fél szabályos háromszög. Emiatt \(\displaystyle BE=2\cdot BD'=2\cdot AD\).

2. megoldás. A feladat trigonometriai eszközökkel is megoldható. Legyen az \(\displaystyle ABC\) háromszög oldala egységnyi. Az \(\displaystyle ADC\) háromszögben alkalmazzuk a szinusztételt és használjuk fel, hogy \(\displaystyle \sin 105^\circ=\sin 75^\circ\).

\(\displaystyle \frac{AD}{AC}=\frac{\sin 15^\circ}{\sin 75^\circ}~~\Longrightarrow~~AD=\frac{\sin 15^\circ}{\sin 75^\circ}=\frac{\sin 15^\circ}{\cos 15^\circ}=\text{tg} 15^\circ.\)

Ugyanebből a háromszögből

\(\displaystyle \frac{CD}{AC}=\frac{\sin 60^\circ}{\sin 75^\circ}~~\Longrightarrow~~CD=\frac{\sin 60^\circ}{\sin 75^\circ}.\)

A következő lépésben az \(\displaystyle ECD\) háromszögre írjuk fel a szinusztételt:

\(\displaystyle \frac{EC}{CD}=\frac{\sin 30^\circ}{\sin 75^\circ}~~\Longrightarrow~~EC=CD\frac{\sin 30^\circ}{\sin 75^\circ}=\frac{\sin 60^\circ\cdot \sin 30^\circ}{\sin^2 75^\circ}.\)

A továbbiakban az addíciós tételek és a nevezetes szögek szögfüggvényei segítségével:

\(\displaystyle AD=\text{tg} 15^\circ=\text{tg} (60^\circ-45^\circ)=\frac{\sqrt{3}-1}{\sqrt{3}+1}=2-\sqrt{3},\)

\(\displaystyle EC=\frac{\frac{\sqrt{3}}{4}}{\left(\frac{\sqrt{6}}{4}+\frac{\sqrt{2}}{4}\right)^2}=\frac{\frac{\sqrt{3}}{4}}{\left(\frac{\sqrt{2}}{4}(\sqrt{3}+1)\right)^2}= \frac{\frac{\sqrt{3}}{4}}{\frac{1}{8}(4+2\sqrt{3})}=\frac{2\sqrt{3}}{4+2\sqrt{3}}=\frac{\sqrt{3}}{2+\sqrt{3}}. \)

Végül az \(\displaystyle EB\) kiszámítása:

\(\displaystyle EB=1-EC=1-\frac{\sqrt{3}}{2+\sqrt{3}}=\frac{2}{2+\sqrt{3}}=2(2-\sqrt{3})=2\cdot AD.\)

Statistics:

156 students sent a solution.
4 points:	118 students.
3 points:	14 students.
2 points:	7 students.
1 point:	3 students.
0 point:	5 students.
Unfair, not evaluated:	3 solutionss.
Not shown because of missing birth date or parental permission:	1 solutions.

Problems in Mathematics of KöMaL, November 2022